Site de simulação de Ótica
https://phet.colorado.edu/sims/html/geometric-optics/latest/geometric-optics_pt_BR.html
Outras simulações:
PhET: Free online physics, chemistry, biology, earth science and math simulations (colorado.edu)
Este trabalho, esta sendo baseado, no treinamento realizado por mim, e adaptado, através do curso que estou fazendo:
https://www.udemy.com/course/deteccao-de-objetos-com-python-e-opencv/
Segue explicação em vídeo:
Este projeto é uma continuação do trabalho colocado no github:
https://github.com/marcelomaurin/hemacias
No programa teste03.py, apresento como capturar a imagem e fiz alguns tratamentos de fundo, usando opencv.
Neste artigo, irei preparar imagens para gerar o reconhecimento da hemácia.

Para tanto fiz a captura da hemácia, através da microscopia. Utilizando um microscópio com lente de ampliação de 20x, com uma câmera USB de 2Mb pixels.

Pegando a figura abaixo:
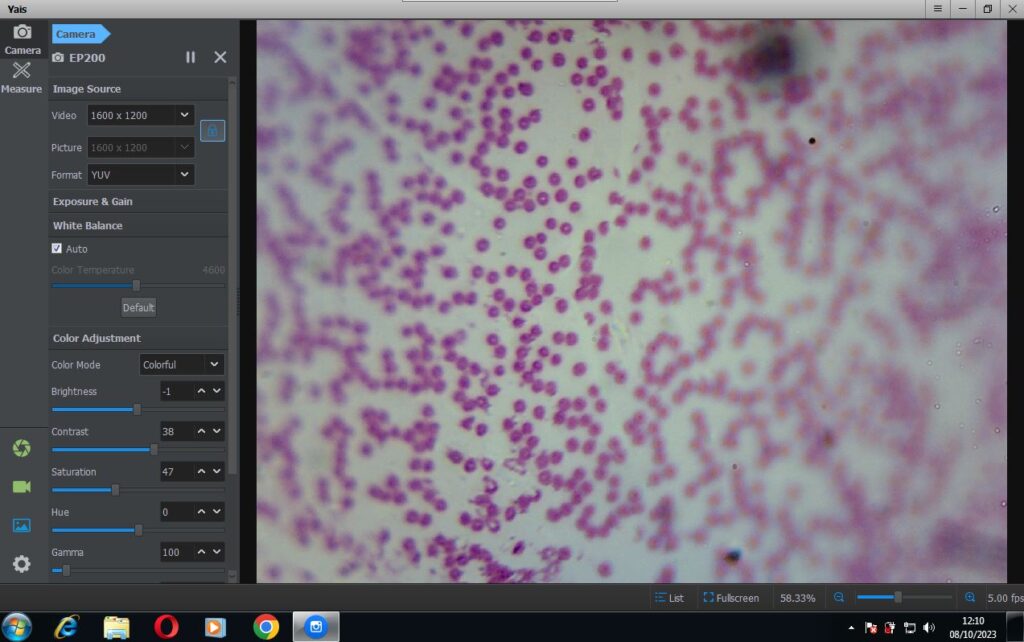
Irei tratar a imagem abaixo, para tentar reconhecer e contar as hemácias.

Para tanto o primeiro trabalho, é trabalhar com a imagem, fazendo duas etapas:
Retirar fundo da imagem da hemácia, e incluí-la em um banco de imagens de fundo.
Neste artigo, irei tratar cada uma destas atividades.
Agora que tenho a imagem, usarei o site
https://www.remove.bg/
Para retirar o fundo da imagem. O procedimento é bem simples, faz-se o upload da imagem já recortada, para o site, e lá retira-se o fundo, com o auxilio de ferramentas do próprio site.
O site é bem intuitivo e pode ser usado livremente.
Ao final criamos a imagem sem o fundo, que iremos utilizar.

A imagem positiva é a imagem que deve possuir a hemácia.

Neste primeiro momento eu preciso de uma base de imagens.
Para isso preciso baixar um grande volume de imagens para gerar tanto imagens positivas como negativas.
Eu peguei as imagem recortada, com os fundos apresentados no aplicativo, e fui recortando montando um banco de imagens coloridos.
Para as imagens de teste, eu peguei imagens de internet e recortei.
Conforme apresentado a baixo:
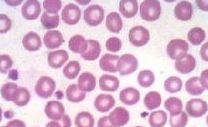
Para ter sucesso, precisarei refazer esse teste, com pelo menos uma dúzia de hemácias, produzindo pelo menos 1000 imagens.
Este trabalho é longo e demorará vários dias.
No próximo artigo iremos processar a imagens de treino, criando uma base real de treinamento.
Apresentação de Eletricidade – materiais tipos
Parte deste material é voltado para estudo pessoal, e foi obtido pelo chatgpt.
Eletricidade: Eletricidade é o conjunto de fenômenos físicos associados à presença e ao fluxo de carga elétrica. Ela pode se manifestar de duas formas principais:
Materiais Elétricos (do ponto de vista da física):


Material isolante
A física da eletricidade é fundamental para a compreensão de muitos aspectos do mundo moderno, desde a iluminação e aquecimento de nossas casas até a operação de dispositivos eletrônicos e comunicações. Essa é uma visão geral do tópico, e cada uma dessas categorias pode ser explorada em profundidade à medida que nos aprofundamos na física dos materiais e na teoria da eletricidade.

M
Para entender melhor o comportamento elétrico dos materiais, vamos começar examinando sua estrutura atômica:
Átomos e Cargas:
Todo átomo é composto por um núcleo (que contém prótons e nêutrons) e elétrons que orbitam o núcleo em camadas chamadas orbitais. Os prótons têm carga positiva, enquanto os elétrons têm carga negativa. Em condições normais, um átomo é neutro, o que significa que tem o mesmo número de prótons e elétrons, resultando em uma carga total de zero.
Tipos de Materiais e Suas Cargas:

No contexto de cargas elétricas e movimento de cargas, a caracterização dos materiais como condutores, isolantes, semicondutores ou supercondutores é crucial. Essas categorias determinam como um material interage com a eletricidade e, portanto, quais aplicações são adequadas para cada tipo de material.
Lei de Coulomb
A Lei de Coulomb descreve a força eletrostática entre duas cargas puntiformes (ou seja, cargas que podem ser consideradas como pontos no espaço). Ela foi formulada pelo físico francês Charles-Augustin de Coulomb em 1785 e é fundamental para o estudo da eletrostática.
História:
Charles-Augustin de Coulomb, nascido em 1736, foi um engenheiro militar e físico francês. Através de seus experimentos precisos com uma balança de torção que ele mesmo inventou, Coulomb foi capaz de formular sua lei sobre a força eletrostática entre cargas. A balança de torção permitiu a ele medir forças muito pequenas entre cargas, e assim, ele pôde quantificar a relação entre a força eletrostática, a distância entre as cargas e a magnitude das cargas.
Princípio da Lei de Coulomb:
A Lei de Coulomb pode ser expressa matematicamente como:
Onde:
Algumas observações sobre a Lei de Coulomb:
A Lei de Coulomb, junto com as leis do eletromagnetismo de Maxwell, forma a base para o entendimento moderno do eletromagnetismo.
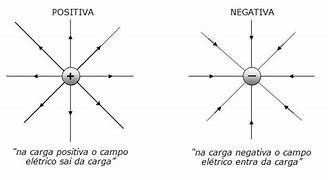
Campo Elétrico
Um campo elétrico é uma descrição do espaço ao redor de uma carga elétrica (ou um sistema de cargas elétricas) no qual outra carga experimentaria uma força elétrica devido à presença da primeira carga. Pode ser visualizado como uma “região de influência” em que a carga cria um efeito.
Definição:
O campo elétrico ( \mathbf{E} ) em um ponto no espaço é definido como a força elétrica ( \mathbf{F} ) que seria exercida sobre uma carga de prova positiva ( q_0 ) colocada naquele ponto, dividida pela magnitude da carga de prova:
[ \mathbf{E} = \frac{\mathbf{F}}{q_0} ]
Direção e Magnitude:
Propriedades:
Campo Elétrico Devido a uma Carga Pontual:
O campo elétrico devido a uma única carga pontual ( q ) é dado por:
onde:
Linhas de Campo Elétrico:
As linhas de campo elétrico são uma representação gráfica usada para visualizar o campo elétrico. As regras para desenhar linhas de campo elétrico incluem:
Efeitos:
Um campo elétrico pode fazer com que cargas se movam, podendo resultar em uma corrente elétrica se essas cargas estiverem em um condutor. Além disso, um campo elétrico pode induzir a polarização de materiais dielétricos, alinhando os dipolos elétricos do material com o campo.
A compreensão do conceito de campo elétrico é crucial para o entendimento de vários fenômenos elétricos e eletromagnéticos na física.
A Lei de Gauss, nomeada em homenagem ao matemático e físico alemão Carl Friedrich Gauss, é uma das leis fundamentais da eletrostática e forma a base para muitos dos cálculos em eletromagnetismo. Ela fornece uma maneira de relacionar a distribuição de carga elétrica a seu campo elétrico resultante.
História:
Carl Friedrich Gauss (1777-1855) foi um dos matemáticos mais influentes da história. Embora seja mais conhecido por seu trabalho em matemática pura, ele também fez contribuições significativas à física. A Lei de Gauss foi primeiramente formulada por ele em 1813, mas foi publicada postumamente em 1867.
Princípios da Lei de Gauss:
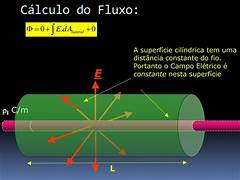
A Lei de Gauss afirma que o fluxo elétrico total através de uma superfície fechada é igual à carga total dentro dessa superfície dividida pela permissividade do vácuo. Matematicamente, ela é expressa como:
[ \oint \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{\text{int}}}{\varepsilon_0} ]
Onde:
Aplicações e Implicações:
A Lei de Gauss, juntamente com as outras equações de Maxwell, fornece uma descrição completa dos fenômenos eletromagnéticos. É uma ferramenta poderosa em física, com aplicações em várias áreas, desde cálculos básicos de campo elétrico até avançadas teorias eletromagnéticas.
Potencial Elétrico
O potencial elétrico é uma quantidade escalar que descreve a capacidade de uma configuração elétrica (geralmente um campo elétrico) de realizar trabalho. É comumente usado para entender diferenças de energia em sistemas elétricos.
Definição:
O potencial elétrico ( V ) em um ponto no espaço é definido como o trabalho realizado pelo campo elétrico ao mover uma carga de prova positiva ( q_0 ) do infinito até esse ponto, dividido pela magnitude da carga de prova:
Unidades:
No Sistema Internacional, o potencial elétrico é medido em volts (V), onde 1 volt é equivalente a 1 joule por coulomb (J/C).
Princípios e Características:
Aplicações:
O conceito de potencial elétrico é fundamental em circuitos elétricos, especialmente quando se trata de componentes como capacitores. Também é essencial na análise de campos elétricos em configurações complexas e na compreensão da diferença de potencial (tensão) em dispositivos elétricos.
Capacitância Elétrica
A capacitância é uma propriedade dos sistemas que permite o armazenamento de energia na forma de um campo elétrico. Os dispositivos projetados para terem uma capacitância específica e utilizados para armazenar e liberar energia elétrica são chamados de capacitores.
Definição:
A capacitância ( C ) de um dispositivo é definida como a razão entre a carga ( Q ) armazenada nele e o potencial elétrico ( V ) ou diferença de potencial (tensão) através dele:
Unidades:
No Sistema Internacional, a unidade de capacitância é o farad (F), onde 1 farad é equivalente a 1 coulomb por volt (C/V).
Princípios e Características:
Aplicações:
Capacitores são componentes essenciais em circuitos eletrônicos. Eles são usados para:
Em sistemas de potência, os capacitores também são usados para corrigir o fator de potência de redes elétricas.
Densidade de Corrente Elétrica
A densidade de corrente elétrica é uma quantidade vetorial que descreve o fluxo de carga elétrica por unidade de área através de um material. Ela é uma medida da quantidade de corrente que passa por uma seção transversal de um material.
Definição:
A densidade de corrente elétrica
Direção:
A direção da densidade de corrente é a direção do fluxo de carga positiva. Em metais, a corrente elétrica é devida ao movimento de elétrons (que são cargas negativas), então a densidade de corrente tem a direção oposta ao movimento dos elétrons.
Unidades:
No Sistema Internacional, a unidade de densidade de corrente é o ampère por metro quadrado
Relação com a Condutividade:
A densidade de corrente pode também ser relacionada com o campo elétrico
Aqui, ( \sigma ) é a condutividade do material (o inverso da resistividade) e ( \mathbf{E} ) é o campo elétrico no material.
Fatores que Afetam a Densidade de Corrente:
Importância e Aplicações:
A densidade de corrente é um conceito crucial em eletrônica e eletromagnetismo. Ela é fundamental no design e análise de dispositivos eletrônicos, no estudo de materiais supercondutores, na descrição de efeitos térmicos em condutores, e em muitas outras áreas da ciência e engenharia.
A resistência elétrica de um condutor pode ser calculada em função da resistividade elétrica do material, juntamente com as dimensões físicas do condutor.
A relação é dada pela seguinte fórmula:
Onde:
Explicação:
A resistividade é uma propriedade intrínseca do material, representando a resistência ao fluxo de corrente elétrica. Materiais com alta resistividade (como borracha ou vidro) são geralmente isolantes, enquanto materiais com baixa resistividade (como cobre ou alumínio) são condutores.
Então, para encontrar a resistência de um condutor com base em sua resistividade, você precisará conhecer as dimensões físicas do condutor e a resistividade do material do qual ele é feito. Usando a fórmula acima, você pode determinar a resistência desse condutor.
F = u * N
u = 6
N= m*g
N = 10 * 10 = 100N
F at = u* N
Fat = 0,6 * 100
Fat = 6-N
2) Um homem tenta levantar uma caixa de 5kg, que está sobre uma mesa, aplicando uma força vertical
de 10N. Nesta situação, qual o valor da força que a mesa aplica na caixa?
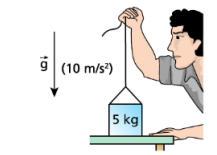
m = 5Kg
P=m * g => 5* 10 = 50N
N= P -F
N = 50 – 10 = 40 N
3) O peso de um objeto na lua é de 48 N. Determine o peso desse objeto na Terra.
Dados: Gravidade da Terra = 10 m/s2
; Gravidade da lua = 1,6 m/s2
Pl = 48N
Pt = ?
g = 10 m/s^2
g = 1,6 m/s^2
Plua = m * g => 48 = m * 1,6 = m = 48/1,6 = 30 kg
Pterra = m * g => 30 * 10 = 300N
4) O alicate da figura é usado para dobrar um fio de cobre. A força motriz aplicada pela pessoa vale 60N.
a) Qual a intensidade da força que comprime o fio? R: 240N
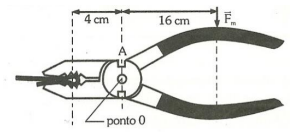
F =Mr = 0
Equilibrio
Mr = Fm * 16 – F * 4 = 0
Fm * 16 = 4F
60 * 16 = 4 F
F = 60 * 16 / 4 => F = 240N
Vm = 240/60 = 4
Vezes maior que a Fm
5) O esquema apresenta uma gangorra homogênea, com seção transversal constante, que tem 7m de
comprimento e está apoiada em C, distante 3m de A. Na extremidade A está uma garota de peso 400 N,
qual é o peso do garoto sentado e B para que a
gangorra fique em equilíbrio na horizontal? R: 300N
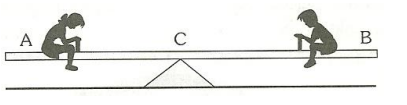
Pa = 400N
Mr = 0
Mr = Pb * 4 – Pa * 3 = 0
Pn * 4 =Pa * 3
Pb * 4 = 400 * 3
Pb = 1200 /4 => Pb = 300N
6) A barra indicada na figura tem peso desprezível e está
em equilíbrio na posição horizontal. Determine x.
R: 2m

F = m * l
500 * x = 200 * 5; pois estão em equilibrio
x = 1000 / 500 => x = 2 m
7) Uma barra rígida, de peso próprio desprezível, é utilizada como alavanca, conforme a figura abaixo. Com a carga suspensa no ponto A, a força 𝐹⃗ que equilibra o sistema vale 200 N. Colocando-se uma outra carga de mesmo valor no ponto B, calcular o valor da nova força necessária para equilibrar o sistema. R: 600
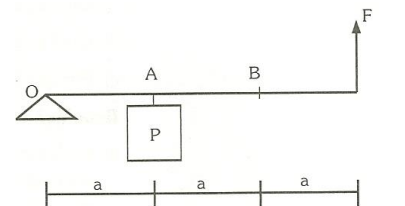
F = m * L
F = 200N
F1 = P * a
F2 = P * a * 3
P2 = 200N
P1 = P2
P1 * a = P2 * a * 3 => P1 = 200 *3 => P1 = 600N
Agora outro bloco P3 = 600N, qual o valor de P2 para o equilibrio
F1 = 600 * a
F2 = N * 3a
F3 = 600 * 2a
F1 + F3 = F2
600* a + 600 * 2a = N * 3a => a * (600+1200) = N * a =>3 N = 600+1200 =>N = 1800/3 => N = 600N
8) Um garoto de 30kg de massa está sentado em um banco, na posição indicada na figura. Desprezando o peso do assento do banco e considerando g = 10 m/s2 , determine a intensidade das forças provocadas nos apoios A e B. R: 60N e 240N
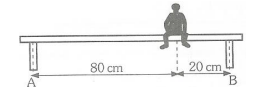
m = 30kg
P6 = 30 * 10 = 300N
No ponto A: Pg * 80 – Nb * 100
No ponto B: Na * 100 – P6 * 20 = 0
300 * 80 = Nb * 100
Nb = 24000/100 => 240N
Na * 100 = 300 * 20
Na = 6000 /100 = 60N
9- A barra da figura tem peso desprezível, é sustentada em A e está em equilíbrio. Calcule a intensidade de 𝐹1 sabendo que 𝐹2 = 12𝑁 e oposicao 𝐹2 = 6𝑁. R: 2,4N
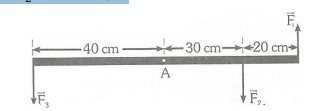
-F1 * 40 + 12N * 70 -6N * 90 = 0
-F1 * 40 +840 – 540 = 0 => F1 = 7.5N
10- A figura indica a posição de um braço humano que tem na palma da mão uma esfera de 4 N.
Calcule o momento dessa força em relação ao ponto O. R: -2,32N.m
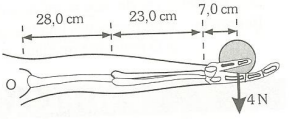
Formula do momento força:
No nosso caso o angulo de 90 graus é 1, ficando
M = 4N * 0,58m => M = 2,32N.m
Portanto o Momento = -2,32Nm
1- Dois blocos M e N, colocados um sobre o outro, estão se movendo para a direita com
velocidade constante, sobre uma superfície horizontal sem atrito. Desprezando-se a
resistência do ar, o diagrama que melhor representa as forças que atuam sobre o corpo M
é:
2- Um bloco é colocado na borda exterior de um carrossel de raio 5,0 m e que dá uma volta
a cada 30 segundos. Para que o bloco permaneça sobre o carrossel, o coeficiente de atrito
deve ser
3- Um bloco com massa de 3 kg está em movimento com aceleração constante na superfície
de uma mesa. Sabendo que o coeficiente de atrito dinâmico entre o bloco e a mesa é 0,4,
calcule a força de atrito entre os dois. Considere g = 10 m/s2
.
4- Um corpo atirado horizontalmente, com velocidade de 10m/s, sobre uma superfície
horizontal, desliza 20m até parar. Adotando g=10m/s2
, o coeficiente de atrito cinético entre
o corpo e a superfície é
a) 0,13
b) 0,25
c) 0,40
d) 0,50
5- A figura a seguir mostra um atleta de ginástica olímpica no aparelho de argolas. O
ginasta encontra-se parado na posição mostrada. Assinale qual dentre as alternativas a
seguir a que melhor representa as forças que atuam sobre ele, desprezando-se as forças
do ar.
6- Um bloco de madeira com massa de 10 kg é submetido a uma força F que tenta colocálo em movimento. Sabendo que o coeficiente de atrito estático entre o bloco e a
superfície é 0,6, calcule o valor da força F necessária para colocar o bloco na situação
de iminência do movimento. Considere g = 10 m/s2
.
7- Uma folha de massa igual 0,3 g cai de uma árvore com velocidade constante. Determine
a força resultante sobre essa folha, sabendo que ela está sujeita à força de resistência do
ar.
Dado: a aceleração da gravidade tem valor igual a 9,8 m/s².
8- O peso de um objeto na lua é de 48 N. Determine o peso desse objeto na Terra.
Dados: Gravidade da Terra = 10 m/s2
; Gravidade da lua = 1,6 m/s2
.
a) 350 N
b) 300 N
c) 200 N
d) 150 N
e) 50 N
9- Duas forças perpendiculares, de 6 N e 8N, são aplicadas a um corpo de massa igual a
20 kg. Determine o módulo da aceleração sofrida por esse corpo considerando que não
haja quaisquer outras forças atuando sobre ele.
10- Um homem tenta levantar uma caixa de 5kg, que está sobre uma mesa, aplicando uma
força vertical de 10N. Nesta situação, qual o valor da força que a mesa aplica na caixa?
11- Uma partícula de massa m é abandonada num plano de inclinação α, num local em que
a aceleração da gravidade tem módulo igual a g. Desprezando o atrito, a aceleração da
partícula, escreva o diagrama de forças (as forças impostas no corpo de massa
12- Um sistema de polias é constituído de modo que a força necessária para içar um objeto
de 1 tonelada é dezesseis vezes menor. Quantas polias soltas existem nessa associação
de polias?
1- Pedro é o filho mais novo de Renata. O garoto reclama a alguns dias de que não consegue
enxergar o que sua professora escreve no quadro-negro, mesmo que ele se sente na primeira
carteira. Ao levar seu filho ao oftalmologista, Renata teve a notícia de que o garoto tinha
dificuldade de enxergar de perto. Assinale a alternativa que contém o nome do problema de
visão e o tipo de lente que vai ajudar Pedro.
a) Hipermetropia, lente esférica
b) Presbiopia, lente convergente
c) Miopia, lente convergente
d) Hipermetropia, lente convergente
e) Estrabismo, lente cilíndrica
Resposta C
2- Ao receber a receita de seus óculos, um paciente leu a seguinte informação:
OD: – 1,0 di
OE: + 1,5 di
Marque a alternativa correta a respeito das informações dadas na receita.
a) No olho direito (OD), o paciente tem hipermetropia, por isso, deve utilizar lentes cilíndricas.
b) No olho esquerdo (OE), o paciente tem hipermetropia, por isso, deve utilizar uma lente
convergente.
c) No olho direito (OD), o paciente tem estrabismo, por isso, deve utilizar uma lente com
vergência negativa.
d) O símbolo “di” significa dioptria e determina o tamanho do foco da lente.
e) No olho esquerdo (OE), o paciente tem presbiopia, por isso, deve utilizar uma lente esférica.
Resposta B
3- Na formação das imagens na retina da vista humana normal, o cristalino funciona como uma
lente:
a) convergente, formando imagens reais, diretas e diminuídas;
b) divergente, formando imagens reais, diretas e diminuídas;
c) convergente, formando imagens reais, invertidas e diminuídas;
d) divergente, formando imagens virtuais, diretas e ampliadas;
e) convergente, formando imagens virtuais, invertidas e diminuídas.
Resposta C
4- A correção para o astigmatismo pode ser feita por:
a) lente esférica convergente;
b) lente esférica divergente;
c) lente esférica côncavo-convexa;
d) lente esférica plano-convexa;
e) lente cilíndrica.
Resposta E
5- O olho humano pode ser considerado um conjunto de meios transparentes, separados um do
outro por superfícies sensivelmente esféricas, que podem apresentar alguns defeitos tais como
miopia, daltonismo, hipermetropia etc. O presbiopismo é causado por:
a) achatamento do globo ocular;
b) alongamento do globo ocular;
c) ausência de simetrias em relação ao eixo ocular;
d) endurecimento do cristalino;
e) insensibilidade ao espectro eletromagnético da luz.
6- O olho humano pode ser entendido como um sistema óptico composto basicamente por duas
lentes – córnea (A) e cristalino (B). Ambas devem ser transparentes e possuir superfícies lisas e
regulares para permitirem a formação de imagens nítidas. Podemos classificar as lentes naturais
de nossos olhos, A e B, respectivamente, como sendo:
a) convergente e convergente.
b) convergente e divergente.
c) divergente e divergente.
d) divergente e convergente.
e) divergente e plana.
Resposta A
7- Uma lente convergente de distância focal d é colocada entre um objeto e uma parede. Para que
a imagem do objeto seja projetada na parede com uma ampliação de 20 vezes, a distância entre
a lente e a parede deve ser igual a:
a) 20/d
b) 20d
c) 19d
d) 21d
e) 21/d
Resposta C
8- Câmeras digitais, como a esquematizada na figura, possuem mecanismos automáticos de
focalização.
Em uma câmera digital que utilize uma lente convergente com 20 mm de distância focal, a
distância, em mm, entre a lente e o sensor da câmera, quando um objeto a 2 m estiver
corretamente focalizado, é, aproximadamente:
a) 1.
b) 5.
c) 10.
d) 15.
e) 20.
Resposta E
Material Anexo
1- Um objeto de 10 cm é colocado a 15 cm de uma lente esférica convexa de distância focal igual a 5 cm. Determine:
Fórmula:
f é a distância focal da lente
v é a distancia da imagem
u e a distancia do objeto à lente
Dado que:
f = 5cm, u = -15cm
Aplicando a equação:
Portanto temos v = 15/4 -> v = 3,75cm
B) Resposta
Portanto a posição da imagem é 3,75cm à direita da lente
c) Característica da imagem
Como o valor de v é positivo, a imagem é real. Como a ampliação é menor do que 1 (0,25), a imagem é diminuída. E, finalmente, como a ampliação é positiva, a imagem está na mesma orientação do objeto.
2- Determine a vergência de uma lente esférica côncava cuja distância focal é igual a 10 cm.
Vergência (V)
f = distancia focal
f = -10 cm ou seja 0,1m.
Aplicando a formula, temos
V = 1 / -0,1 => V = -10
Portando a medida é 10 dioptrias.
3- Uma lente, feita de material cujo índice de refração absoluto é 1,5, é convergente no ar. Quando
mergulhada num líquido transparente, cujo índice de refração absoluto é 1,7, ela:
a) será convergente;
b) será divergente;
c) será convergente somente para a luz monocromática;
d) se comportará como uma lâmina de faces paralelas;
e) não produzirá nenhum efeito sobre os raios luminosos.
Resposta B
4- Um objeto está sobre o eixo óptico e a uma distância p de uma lente convergente de distância f. Sendo
p maior que f e menor que 2f, pode-se afirmar que a imagem será:
a) virtual e maior que o objeto;
b) virtual e menor que o objeto;
c) real e maior que o objeto;
d) real e menor que o objeto;
e) real e igual ao objeto.
5- Um objeto real é colocado perpendicularmente ao eixo principal de uma lente convergente de distância
focal f. Se o objeto está a uma distância 3f da lente, a distância entre o objeto e a imagem conjugada
por essa lente é:
a) f/2
b) 3f/2
c) 5f/2
d) 7f/2
e) 9f/2
Dado:
f = f
u = -3f
Ficando 3 = 3f(1/v) -1 => v = 3f/4 => v 0,75f
d = u +v
d = -3f + 0,75f => d = 2,25f
D = 2,25 f
d = 2,25f
Portanto, a distância entre o objeto e a imagem é 2,25f = 9f /4
ficando igual a 2f + f/4 = 2,25f o que é equivalente 5f/2

Primeiramente, gostaria de dizer que não sou especialista em Pentaho, e que estarei escrevendo este artigo, como forma de estudo.
Pentaho é uma ferramenta de BI (business intelligence) desenvolvida pela Hitachi Vantara.
O site oficial do Pentaho é :
https://www.hitachivantara.com/en-us/products/pentaho-platform/data-catalog.html
Os softwares oficiais do pentaho, estão no próprio site do fabricante e também no git.
Neste modelo, podemos ver como as coisas funcionam.
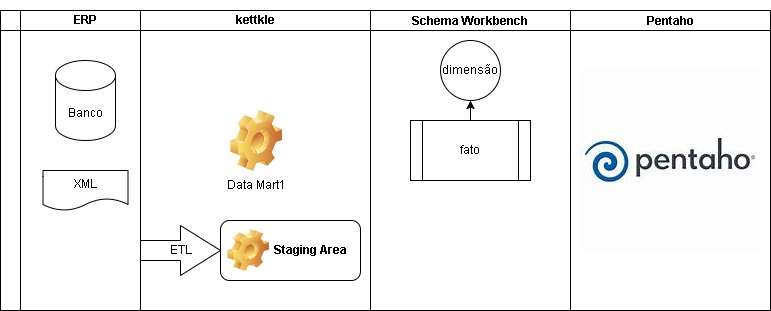
O ERP que possui os dados se conecta com a ferramenta kettkle, que extrai os dados gerando os data marts que são grandes grupos de dados extraídos do ERP.
Após importados os dados do ERP, o Schema Workbench gera e processa os dados em dimensões de dados. Que a grosso modo são os dados trabalhados, para um dado objetivo. Exemplo processamento de dados em dimensão de tempo (classificando em hierarquias como ano, mes , trimestre , etc.).
Por fim, a partir dos dados criados no schema são consumidos em OLAPs usando o Pentaho para criar relatórios e analises, dashboards.
O termo “Kettle” refere-se a “K.E.T.T.L.E.”, que é um acrônimo para “Kettle Extraction Transformation Transport Load Environment”. Kettle é o nome original do projeto que agora é mais comumente conhecido como “Pentaho Data Integration” (PDI).
O PDI/Kettle é uma ferramenta de integração de dados open-source.
Ele fornece funcionalidades ETL (Extract, Transform, Load – Extração, Transformação e Carga), permitindo aos usuários definir processos para extrair dados de várias fontes, transformá-los conforme necessário e, em seguida, carregá-los em sistemas de destino, como bancos de dados, data warehouses, ou outras aplicações.
O Kettle foi projetado para ser flexível e extensível, suportando uma ampla variedade de fontes de dados e destinos, transformações e operações de carga. A interface gráfica do PDI permite que os usuários “desenhem” seus processos ETL, arrastando e soltando componentes e conectando-os para definir fluxos de dados.
Algumas características notáveis do Kettle/PDI incluem:
O Kettle foi um dos componentes principais da suíte Pentaho quando esta foi lançada. Com o tempo, o nome “Kettle” foi um pouco ofuscado em favor de “Pentaho Data Integration”, mas muitos ainda usam os termos de forma intercambiável, especialmente aqueles que têm experiência com as versões mais antigas da ferramenta.
O “Schema Workbench” é uma ferramenta associada ao Pentaho Analysis Services (também conhecido como Mondrian).
Sua principal função é fornecer uma interface gráfica para a criação e edição de esquemas OLAP (On-Line Analytical Processing). Estes esquemas definem cubos, dimensões, hierarquias e medidas que são usadas para criar consultas multidimensionais e análises em dados armazenados em bancos de dados relacionais.
Aqui estão alguns pontos-chave sobre o papel do Schema Workbench:
O Schema Workbench simplifica a tarefa de definir e organizar a estrutura dos dados para análise OLAP, tornando mais fácil para os desenvolvedores e analistas de BI criar soluções de análise robustas usando o Pentaho/Mondrian.
O Pentaho fornece um ecossistema integrado de ferramentas para business intelligence, desde a integração de dados até a visualização. O Schema Workbench, associado ao Pentaho Analysis Services (Mondrian), é usado para criar esquemas OLAP que definem como os dados são estruturados para análise multidimensional. Depois de definir um esquema com o Schema Workbench, ele pode ser usado no Pentaho para criar relatórios, análises e dashboards.
Aqui está uma visão geral de como os dados dos esquemas criados no Schema Workbench são visualizados no Pentaho:
Em resumo, o Schema Workbench é usado para definir a estrutura dos dados para análise multidimensional. Uma vez definidos e publicados, esses esquemas são a base para a criação de análises, relatórios e dashboards no ecossistema Pentaho, permitindo aos usuários visualizar e explorar seus dados de várias maneiras.
1- Uma lente plano-convexa imersa no ar (n=1,0) apresenta índice de refração de 1,4 e raio de curvatura igual a 10cm. Assinale , entre as alternativas a seguir, aquela que corresponde a distancia focal dessa lente.
a) 25m
b 0,25m
c) 0,5m
d) 0,05m
e) 0,4m
Dado que a lente está imersa no ar com índice de refração =1n ar=1, então:
1/f = (1,4 -1) (1/10 -0)
1/f = 0,4 * 0,1
1/f = 0,04
Então 0,04f= 1=> 25 cm ou em metros 0,25m , resposta B
Duas lentes delgadas e convergentes, de distâncias focais f1=10cm e f2=40cm , foram justapostas para se obter uma maior vergência. Qual a convergência obtida com essa associação é , em dioptrias? (Lembrando que Ct= C1 + C2)
Onde :
f é a distancia focal da lente (metros)
C é a convergência da lente (em dioptrias)
Dado que:
f1 = 10cm = 0,1m
f2 = 40cm = 0,4m
Então as convergências da lentes são
C1= 1/f1 => 1/0,1 = 10D
C2 = 1/f2 => 1/0,4 = 2,5 D
A convergência total Ct para duas lentes justapostas é a soma das suas convergencias individuais:
Ct = C1 + C2
Ct = 10D + 2,5D
Ct = 12,5 D
Portanto, a convergência obtida com essa associação é 12,5 dioptrias.
Trabalho para 29/09/2023
Um capacitor consegue armazenar cargas de até 1 nC para uma diferença de potencial entre suas placas de 1 mV, Calcule o módulo da capacitância desse dispositivo.
Resposta:
Baseado na função
Onde C é a capacitância em Farads.
Q é a carga armazenada em Coulombs C
V é a voltagem Volts
Substituindo
Q = 1nC e V= mV
Resolvendo a questão
ou C = 1 uF