Trabalho de Processamento de Sinais
Link do trabalho:
Aluno: Marcelo Maurin Martins
Número FATEC: 2840612223009
e-mail:marcelo.martins34@fatec.sp.gov.br
Base do Codigo
import numpy as np
import matplotlib.pyplot as plt
import os
import cv2
import numpy as np
from scipy.io import loadmat
from IPython.display import HTML
from base64 import b64encode
from matplotlib import pyplot as plt
import ipywidgets as widgets
from IPython.display import displayExercício 1
# Carregar a imagem
image_path = 'xc.tif' # Substitua pelo caminho da sua imagem
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
# Verificar se a imagem foi carregada corretamente
if image is None:
raise ValueError("A imagem não pôde ser carregada. Verifique o caminho fornecido.")
# Calcular o histograma
histogram = cv2.calcHist([image], [0], None, [256], [0, 256])
# Plotar o histograma
plt.figure()
plt.title("Histograma")
plt.xlabel("Intensidade")
plt.ylabel("Número de Pixels")
plt.plot(histogram)
plt.xlim([0, 256])
plt.show()
# Sliders para ajustar os valores de c e b
c_slider = widgets.FloatSlider(value=1.0, min=0.1, max=3.0, step=0.1, description='c')
b_slider = widgets.IntSlider(value=0, min=-100, max=100, step=1, description='b')
# Interagir com os sliders
widgets.interact(update_image, c=c_slider, b=b_slider)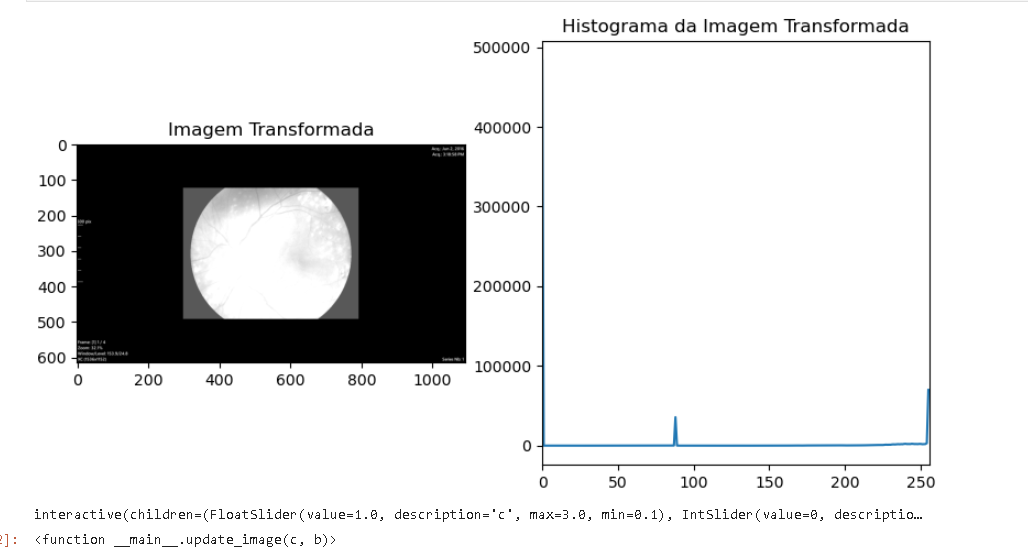
Transformação de intensidades (Nota: 3.0/10.0)
# Carregar a imagem
image_path = 'xc.tif' # Substitua pelo caminho da sua imagem
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
# Verificar se a imagem foi carregada corretamente
if image is None:
raise ValueError("A imagem não pôde ser carregada. Verifique o caminho fornecido.")
# Calcular o histograma
histogram = cv2.calcHist([image], [0], None, [256], [0, 256])
# Plotar o histograma
plt.figure()
plt.title("Histograma")
plt.xlabel("Intensidade")
plt.ylabel("Número de Pixels")
plt.plot(histogram)
plt.xlim([0, 256])
plt.show()
# Função para ajustar os valores de c e b e aplicar na imagem
def adjust_image(c, b):
adjusted_image = cv2.convertScaleAbs(image, alpha=c, beta=b)
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.title("Imagem Ajustada")
plt.imshow(adjusted_image, cmap='gray')
plt.axis('off')
# Calcular o histograma da imagem ajustada
adjusted_histogram = cv2.calcHist([adjusted_image], [0], None, [256], [0, 256])
plt.subplot(1, 2, 2)
plt.title("Histograma Ajustado")
plt.xlabel("Intensidade")
plt.ylabel("Número de Pixels")
plt.plot(adjusted_histogram)
plt.xlim([0, 256])
plt.show()
# Sliders para ajustar os valores de c e b
c_slider = widgets.FloatSlider(value=1.0, min=0.1, max=3.0, step=0.1, description='c')
b_slider = widgets.IntSlider(value=0, min=-100, max=100, step=1, description='b')
# Interagir com os sliders
widgets.interact(adjust_image, c=c_slider, b=b_slider)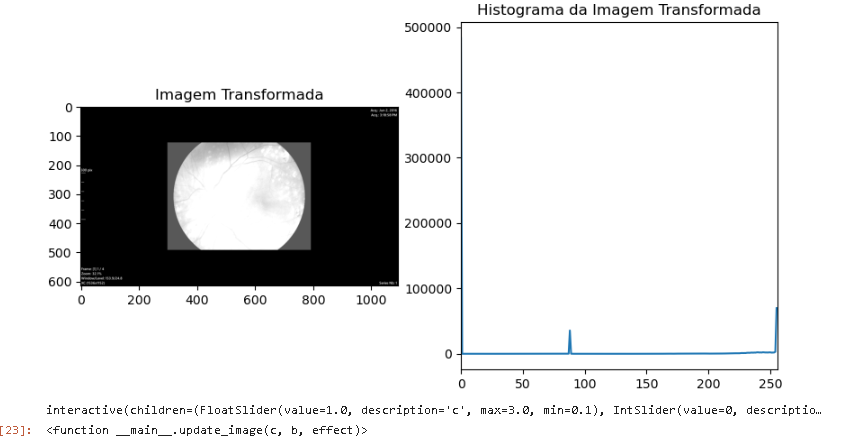
Exercicio 2.1
import numpy as np
import matplotlib.pyplot as plt
import cv2
import ipywidgets as widgets
from IPython.display import display
# Carregar a imagem
image_path = 'tomo.tif' # Substitua pelo caminho da sua imagem
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
# Verificar se a imagem foi carregada corretamente
if image is None:
raise ValueError("A imagem não pôde ser carregada. Verifique o caminho fornecido.")
# Função para ajustar os valores de c e b e aplicar na imagem
def adjust_image(c, b):
adjusted_image = cv2.convertScaleAbs(image, alpha=c, beta=b)
plt.figure(figsize=(12, 6))
plt.subplot(1, 3, 1)
plt.title("Imagem Ajustada")
plt.imshow(adjusted_image, cmap='gray')
plt.axis('off')
# Calcular o histograma da imagem ajustada
adjusted_histogram = cv2.calcHist([adjusted_image], [0], None, [256], [0, 256])
plt.subplot(1, 3, 2)
plt.title("Histograma Ajustado")
plt.xlabel("Intensidade")
plt.ylabel("Número de Pixels")
plt.plot(adjusted_histogram)
plt.xlim([0, 256])
# Aplicar efeito negativo
negative_image = 255 - adjusted_image
negative_histogram = cv2.calcHist([negative_image], [0], None, [256], [0, 256])
plt.subplot(1, 3, 3)
plt.title("Imagem Negativa")
plt.imshow(negative_image, cmap='gray')
plt.axis('off')
plt.figure(figsize=(6, 4))
plt.title("Histograma da Imagem Negativa")
plt.xlabel("Intensidade")
plt.ylabel("Número de Pixels")
plt.plot(negative_histogram)
plt.xlim([0, 256])
plt.show()
# Sliders para ajustar os valores de c e b
c_slider = widgets.FloatSlider(value=1.0, min=0.1, max=3.0, step=0.1, description='c')
b_slider = widgets.IntSlider(value=0, min=-100, max=100, step=1, description='b')
# Interagir com os sliders
widgets.interact(adjust_image, c=c_slider, b=b_slider)
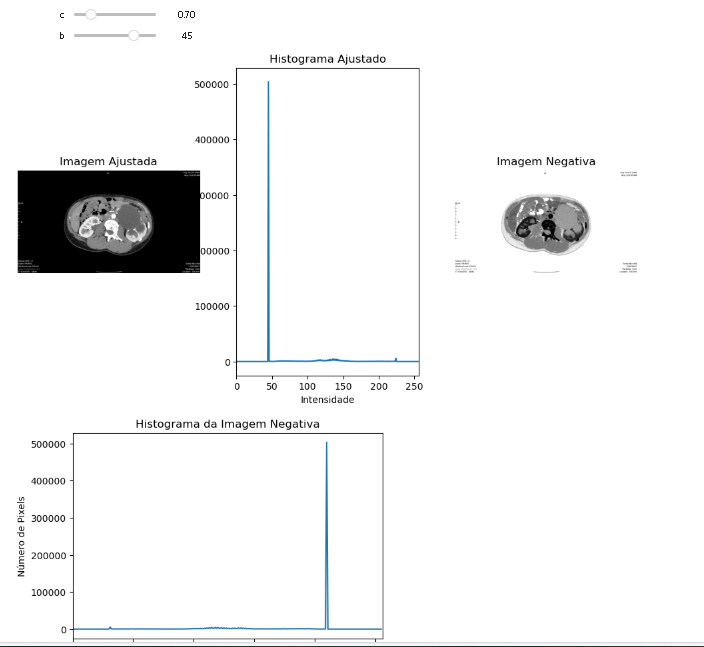
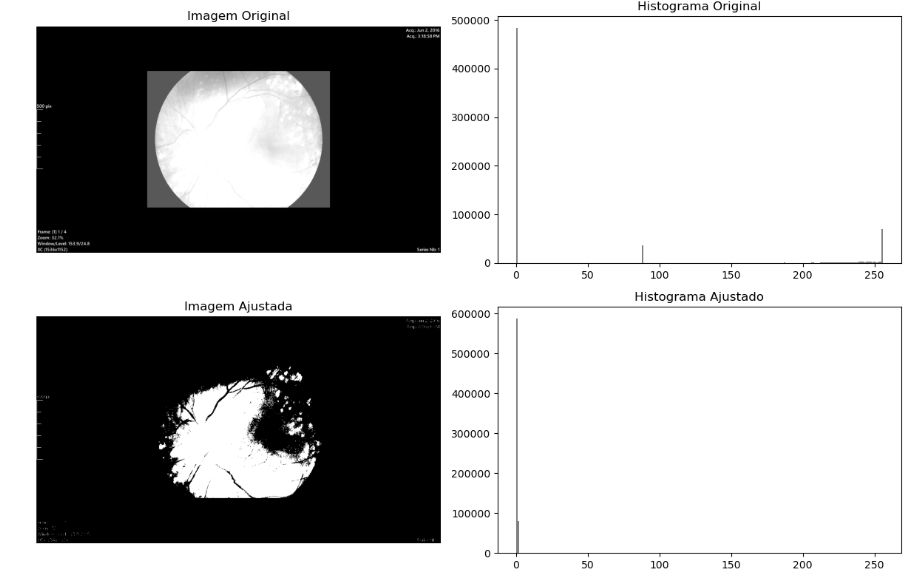
Exercicio 3 – Restauração da Imagem
# Função para ajustar brilho e contraste
def ajustar_brilho_contraste(imagem, alpha, beta):
nova_imagem = cv2.convertScaleAbs(imagem, alpha=alpha, beta=beta)
return nova_imagem
# Carregar a imagem
imagem = cv2.imread('xc.tif', cv2.IMREAD_GRAYSCALE)
# Ajuste de brilho e contraste
alpha = 0.002 # Contraste
beta = 0.002 # Brilho
imagem_ajustada = ajustar_brilho_contraste(imagem, alpha, beta)
# Plotar as imagens e os histogramas
fig, axs = plt.subplots(2, 2, figsize=(12, 8))
# Imagem original
axs[0, 0].imshow(imagem, cmap='gray')
axs[0, 0].set_title('Imagem Original')
axs[0, 0].axis('off')
# Histograma da imagem original
axs[0, 1].hist(imagem.ravel(), bins=256, range=(0, 256), color='gray')
axs[0, 1].set_title('Histograma Original')
# Imagem ajustada
axs[1, 0].imshow(imagem_ajustada, cmap='gray')
axs[1, 0].set_title('Imagem Ajustada')
axs[1, 0].axis('off')
# Histograma da imagem ajustada
axs[1, 1].hist(imagem_ajustada.ravel(), bins=256, range=(0, 256), color='gray')
axs[1, 1].set_title('Histograma Ajustado')
plt.tight_layout()
plt.show()