Trabalho de MathLab

Projetos de Sistemas de Controle com o Matlab

DISCIPLINA /AVALIAÇÃO: Tecnologia de Automação I / P1
Grupo: 1
Nome: Marcelo , Robson
Professor: Marcelo Duarte

(4,0 pontos) Projeto de Controladores PID.

Considere um sistema de controle em malha fechada com realimentação unitária em que a planta é de segunda ordem com a seguinte função de transferência

𝐺𝑝(𝑆) =

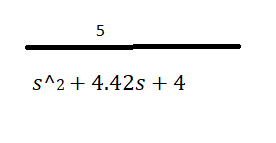
(1,0 ponto) Encontre a função de transferência em malha fechada e verifique graficamente a resposta ao degrau com o MATLAB.

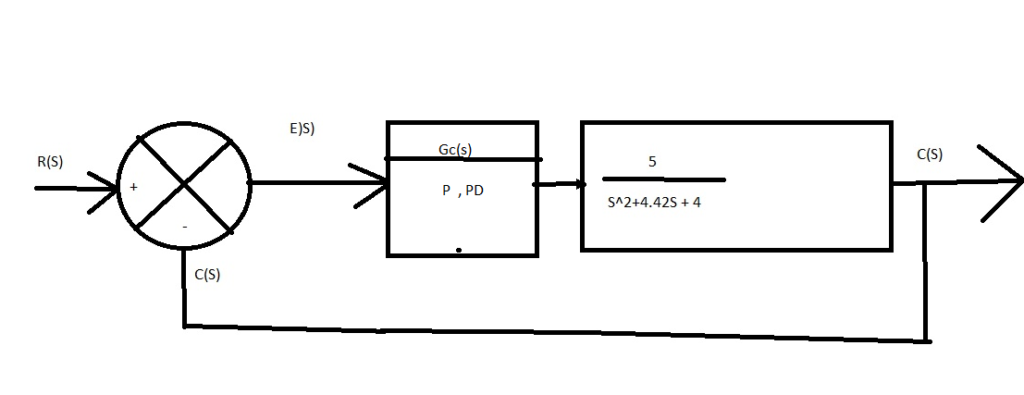
Integre a esta planta do sistema em malha fechada a controladores do tipo PID de acordo com as DUAS alternativas a seguir. 

a) Controlador Proporcional (P)

𝐺𝑟𝑢𝑝𝑜 01

𝐾_𝑝 = 36

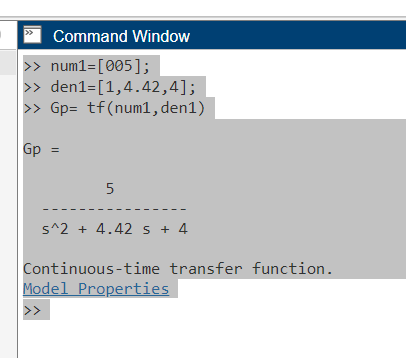
Onde fica num1 o 5

a função ficaria 1, do S^2-> 1S^2 -> 1;

o 4.42 S -> ficaria como segundo nro.

e o ultimo o nro 4.

Ficando [1,4.42,4]

>> num1=[005];
>> den1=[1,4.42,4];
>> Gp= tf(num1,den1)

Gp =
 
         5
  ----------------
  s^2 + 4.42 s + 4
 
Continuous-time transfer function.Model Properties
>> 

Agora vamos montar o grafico.

ft1 = feedback(Gp,1);

step(ft1);

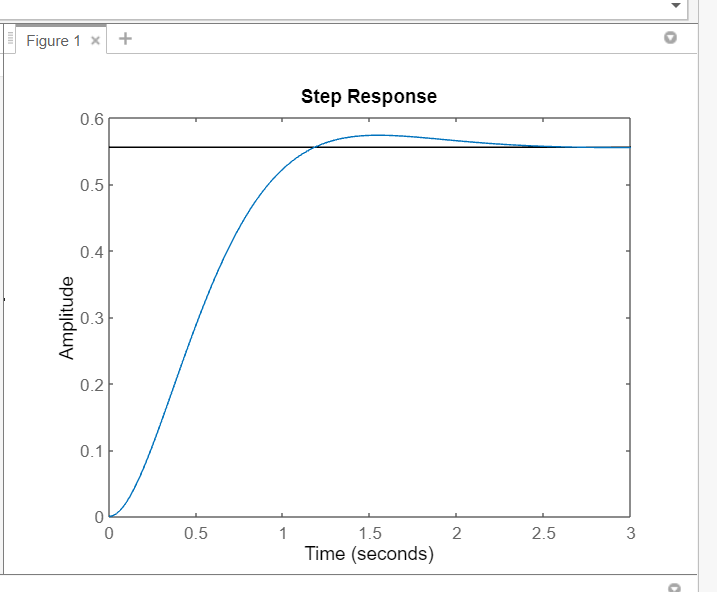
a) Controlador Proporcional (P)

𝐺𝑟𝑢𝑝𝑜 01

𝐾_𝑝 = 36

Parte 2

|Gc(s) = Kp

Gc(s) = Kp+kdS

TEMOS A função:

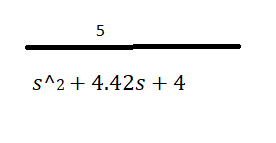
Criamos a segunda função, pela multiplicação do Gc * Gp:

Onde obtemos a função G10:

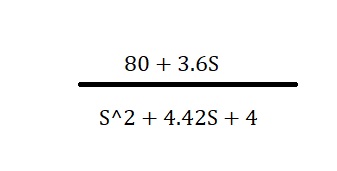
Kp = 36;
Kd= 0,2 * Kp;


num4=[005];
den4=[1,4.42,4];
Gp4= tf(num1,den1);


%PD = Kp+ Kd * Gp4b ;
%Gp5 = PD * Gp4;

num10=[0,3.6,80];
den10=[1,4.42,4];
G10= tf(num10,den10);
G_fechado= feedback(G10,1);

De posse destas informações

Geramos o gráfico abaixo:

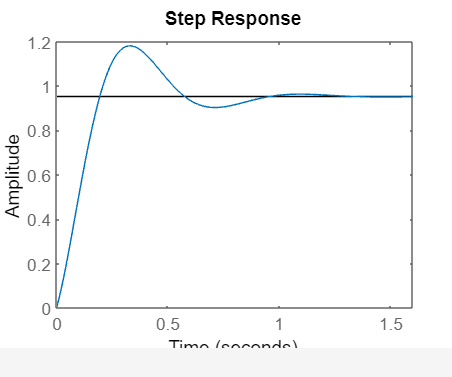
b) Controlador Proporcional Derivativo (PD)

Conforme apresentado em:

http://www.ece.ufrgs.br/~jmgomes/pid/Apostila/apostila/node29.html

O Controlador Proporcional-Derivativo (PD)

A ação derivativa quando combinada com a ação proporcional tem justamente a função de “antecipar” a ação de controle a fim de que o processo reaja mais rápido. Neste caso, o sinal de controle a ser aplicado é proporcional a uma predição da saída do processo.

𝐺𝑟𝑢𝑝𝑜 01
𝐾𝑝 = 36
𝐾𝑑 = 2% 𝑑𝑒 𝐾p

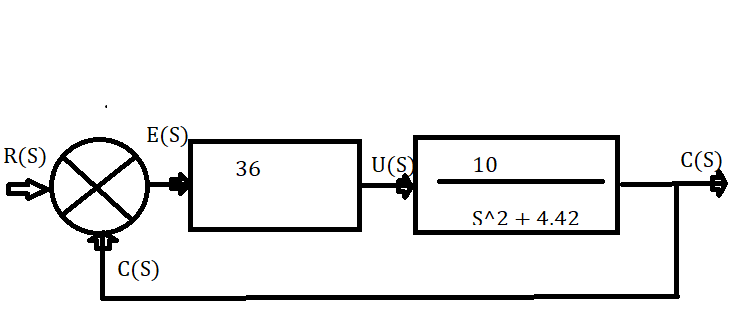
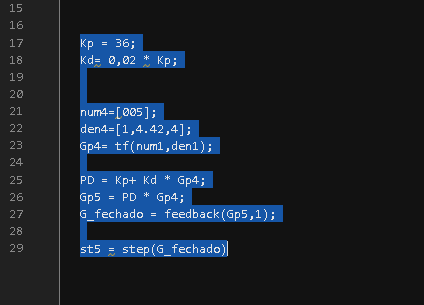
Kp = 36;
Kd= 0,02 * Kp;


num4=[005];
den4=[1,4.42,4];
Gp4= tf(num1,den1);

PD = Kp+ Kd * Gp4;
Gp5 = PD * Gp4;
G_fechado = feedback(Gp5,1);

st5 = step(G_fechado)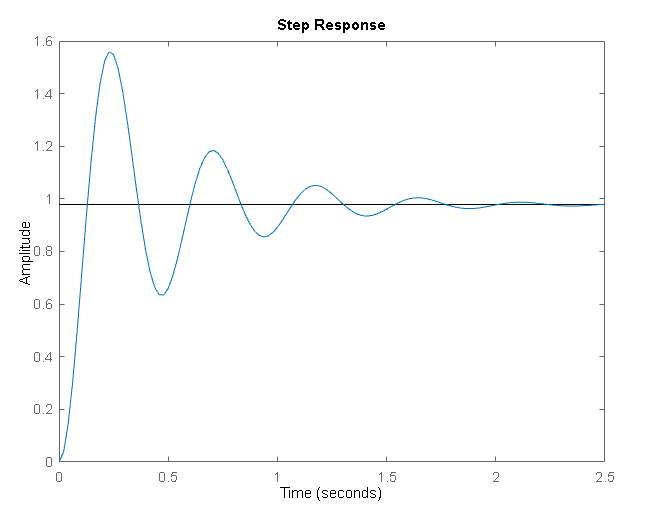

2) Projeto de controle de aplicação de insulina

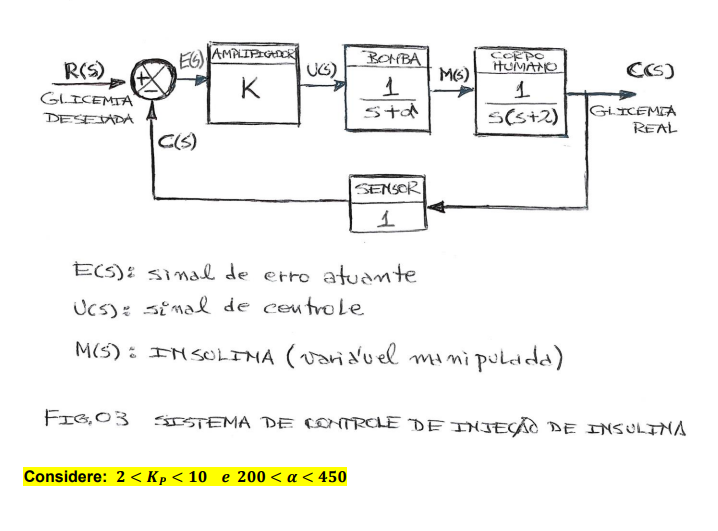
Ficando no Mathlab , conforme apresentado:

s=tf('s');
num6=[1];
den6=[1,2];
uGp6=tf(num6,den6);

num7=[1];
den7=[1,2];
mGp7=tf(num7,den7);

G8=series(uGp6,mGp7);
ft9=feedback(G8,1);
impulse(ft9);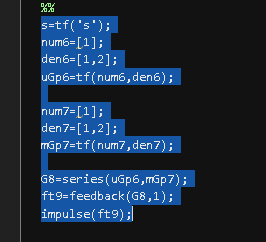

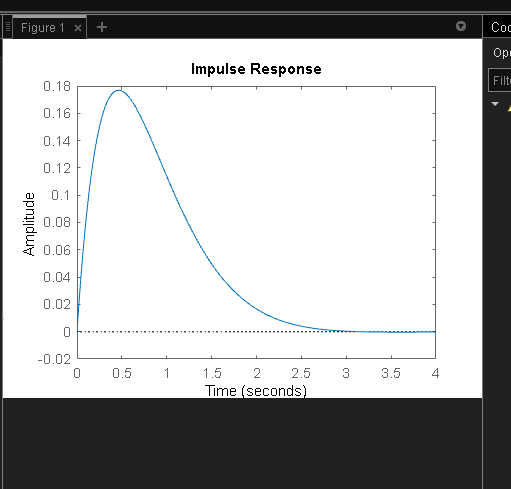
Considerando o Kp ; 2< Kp < 10

e 200 < a 450

Considerando kp=2, e a =200

s=tf('s');

num6=[1];

a=200;

den6=[1,a];

uGp6=tf(num6,den6);

num7=[1];

den7=[1,2];

mGp7=tf(num7,den7);

G8=series(uGp6,mGp7);

G9= Kp*G8;

ft9=feedback(G9,1);

impulse(ft9);

3 ) Sistema de controle em malha lenta

Uma das formas clássicas de se fazer o controle de potência de uma cavidade laser e mostrada na figura 47. O Diodo laser de bombeio, o cristal laser e o cristal SHG formam a cavidade laser. Através da injeção corrente no diodo de bombeio é possível obter um feixe de laser amarelo. O controle da cavidade é efetuado por dois controladores PI ( Proporcional integrative) (OGOTA,2003), PI 1 e P3, ligados numa configuração do tipo cascata ( SEDRA et a.,2007). A malha de controle formada pelo sensor HALL (sensor corrente), PI e 3 MOSFET  ( field-effect transitor) (SEDRA.,2007) garante que o diodo bombeie o cristal com uma potência óptica proporcional ao sinal de referência aplicado na entrada da malha de controle. Para evitar flutuações de potência na saída da cavidade, existe uma malha de controle externa que capta uma percentagem da potência atraves do fotodiodo e realimenta o controlador PI 3.O resultado dessa topologia é a relação linearmente proporcional entre a referência de tensão gerada pelo microcontrolador e a potência óptica na saída da cavidade.

Essa arquitetura de controle possui algumas limitações quando se necessita geral pulso da ordem microssegundos. A primeira causa é o atraso gerado pelo PI 3 e PI 1, visto que a saída de um controlador é usada como entrada para outro. A segunda causa é a fonte de alimentação que possui um tempo de resposta a variação de uma carga muito lenta que pode chegar 1ms, quando utilizada a potência máxima da fonte. A terceira causa é a indutância dos cabos de alimentação do diodo laser que responde a variação da corrente com uma variação de tensão parasita. Cargas sensíveis tais como diodo laser são susceptíveis  a essas variações e podem ter junção PN danificada. Essa topologia é adotada no controle do laser no modo  normal de aplicação laser (regime continuo), no qual os pulso possuem duração longa, entre 50ms e 1000ms.