Trabalho de Eletricidade
Reposição de aula.
Marcelo Maurin Martins
Questão 1
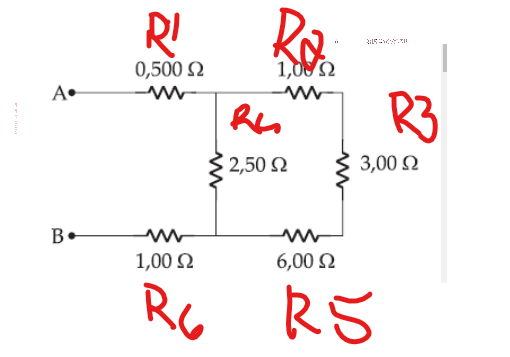
Primeiro R235 = 1+ 3 + 6 => 10ohms
Segundo
R4235 = 1\req = 1 \2,5 + 1\ 10 => 4\10 + 1\10 => 5\10 -> 0,5ohmsPor fim a ultima parte
R123456 -> 0,5 + 0,5 + 1 => 2ohmsResposta Req 2ohms.
Questão 2
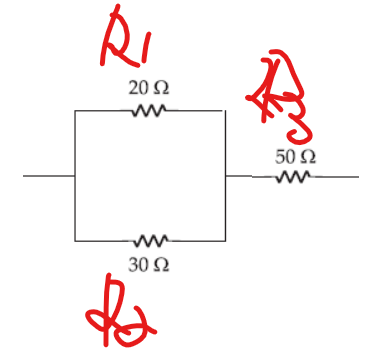
R12 = 1/20 + 1/30 => 3\60 +2\60 => 5\60 ohms = req = 12ohms
R123 => 12 +50 => 62ohmsQuestão 3
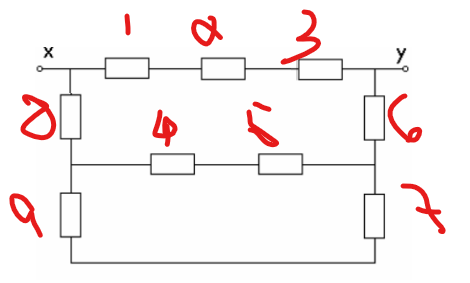
R123 => 10 + 10 + 10 => 30 ohmsR4586 => 40ohms1\R1234568 => 1\30 + 1\40 => 4\120 + 3\120 => 7\120 =R97 = 20ohms1\R123456789 =120\7 + 1\20 => 2400\140 + 7\140 => 2407\140=> 0,058ohms4) questão
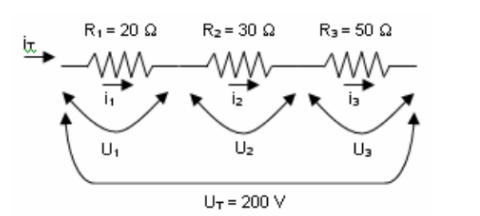
R123 = 20+ 30 + 50 = 100ohms
Resposta A 100 ohms
V = R * i => 200 = 100 * i => i = 200\100 => 2AResposta B 2ª pois em um circuito em serie a corrente é a mesma.
C)
V1 = 20 * 2 = 40VV2 = 30* 2 = 60VV3= 50*2 = 100VQuestão 5
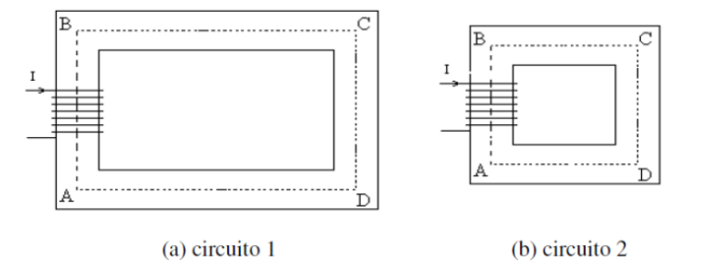
Calcular a intensidade de campo induto
Nro espiras 200
Corrente 1ª
Vamos considerar que o circuito 1 tenha um comprimento médio de 20 cm (0,2 m) e o circuito 2 tenha um comprimento médio de 10 cm (0,1 m).
Ambos os circuitos têm 200 espiras e são percorridos por uma corrente de 1 A.
Para um solenoide retangular, a intensidade do campo indutor pode ser aproximada usando a fórmula de Ampère para um solenoide ideal:
B = μ₀ * n * Ionde B é a intensidade do campo indutor, μ₀ é a permeabilidade magnética do vácuo (aproximadamente 4π × 10⁻⁷ Tm/A), n é o número de espiras por unidade de comprimento e I é a corrente que passa pelas espiras.
Primeiro, vamos calcular o número de espiras por unidade de comprimento para cada circuito:
Circuito 1:
n1 = N / L1 n1 = 200 espiras / 0,2 m n1 = 1000 espiras/mCircuito 2:
n2 = N / L2 n2 = 200 espiras / 0,1 m n2 = 2000 espiras/mAgora podemos calcular a intensidade do campo indutor para cada circuito usando a fórmula de Ampère:
Circuito 1:
B1 = μ₀ * n1 * I B1 = (4π × 10⁻⁷ Tm/A) * (1000 espiras/m) * (1 A) B1 ≈ 1,26 TCircuito 2:
B2 = μ₀ * n2 * I B2 = (4π × 10⁻⁷ Tm/A) * (2000 espiras/m) * (1 A) B2 ≈ 2,52 TPortanto, a intensidade do campo indutor para o circuito 1 é aproximadamente 1,26 T e para o circuito 2 é aproximadamente 2,52 T.
