Física II – 16/09
A impedância acústica é uma propriedade fundamental em acústica e ultrassonografia que descreve a resistência de um material à propagação de uma onda acústica. Ela é definida como o produto da densidade do material (ρ) e a velocidade da onda sonora (c) no material. Matematicamente, pode ser expressa como:
[ Z = \rho \times c ]
Onde:
- ( Z ) é a impedância acústica (geralmente medida em ( \text{Rayls (Pa.s/m)} ) ou ( \text{kg/m}^2\text{s} )),
- ( \rho ) é a densidade do material (geralmente medida em ( \text{kg/m}^3 )),
- ( c ) é a velocidade da onda sonora no material (geralmente medida em ( \text{m/s} )).
A impedância acústica é crucial para determinar como as ondas acústicas interagem com interfaces entre diferentes materiais. Quando uma onda sonora encontra uma interface entre dois materiais com diferentes impedâncias acústicas, parte da onda é refletida e parte é transmitida. A diferença na impedância acústica entre os dois materiais determinará a proporção de onda refletida em relação à transmitida. Essa propriedade é fundamental, por exemplo, na geração de imagens por ultrassom, onde os contrastes nas imagens são frequentemente devido às diferenças na impedância acústica entre os tecidos.
A atenuação sonora refere-se à redução na intensidade ou amplitude de uma onda sonora à medida que ela se propaga através de um meio. Há várias razões para essa diminuição da amplitude ou energia da onda sonora:
- Absorção: À medida que o som viaja através de um meio, como o ar, parte de sua energia é absorvida pelo próprio meio e convertida em outras formas de energia, como calor.
- Difusão ou dispersão: As ondas sonoras podem se espalhar em várias direções, especialmente quando encontram obstáculos ou são refletidas em superfícies irregulares.
- Reflexão: Quando ondas sonoras encontram uma superfície ou interface, parte da energia sonora pode ser refletida de volta, dependendo das propriedades acústicas da superfície.
- Refracção: Mudanças na direção das ondas sonoras devido a variações na velocidade do som em diferentes partes do meio também podem causar atenuação.
- Difração: As ondas sonoras podem se curvar em torno de obstáculos, o que pode causar uma diminuição na intensidade do som em determinadas direções.
- Condução: Em alguns casos, a energia sonora pode ser conduzida para longe da fonte através de um meio sólido, como uma parede ou piso, levando à atenuação do som no ambiente original.
A atenuação sonora é especialmente importante em diversas áreas, como acústica arquitetônica (para design de espaços silenciosos ou teatros), engenharia ambiental (para controlar o ruído urbano) e design de equipamentos de áudio.
Em muitos contextos, quando falamos sobre materiais “isolantes acústicos”, estamos nos referindo a materiais que são eficazes em causar atenuação sonora, reduzindo assim a transmissão de energia sonora de um local para outro.
Exercícios

Solução:

R= Ir/Io = (Za-Zb)^2 / (Za+Zb)^2
4) Uma onda ultrassonica de 3,5 Mhz incide sobre o musculo biceps, no qual o coefiente de atenuação A vale 0,6 cm ^3 . De quanto por cento de intensidade do ultrassom será atenuada a 1cm do ponto de incidência?
I = Io * e ^2slphs x
alpha = 0,6 cm ^-1
x = 1 cm
I/I0 = e -2 alpha *x
I/I0= e^-1,2 = 0,30 ou 30%
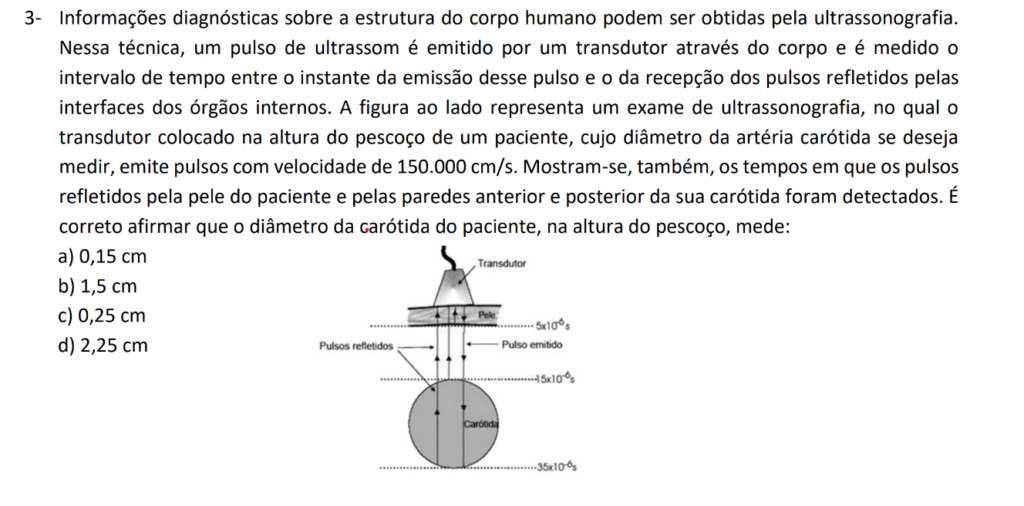
V = Delta S / Delta t
V = 150000 cm /s
Delta S = ?
Delta t = 35 * 10 ^-6 – 5 * 10 ^-6 = 30 * 10 ^-6 segundos
Delta t interno= 15 * 10 ^-6 = 10 * 10 ^-6 s
Delta ext = 150000 * 30 * 10 ^-6 => 45 * 10 ^-6 * 10 ^5 = 45 * 10 ^-1 cm
Delta s int = 150000 * 10 * 10^-6 = 16 * 10 -1 cm
Delta s = 45* 10 ^-1 – 15* 10 ^-1 = 30 * 10 ^- 1 => 3 xm

Formula de Decibeis
Delta = 0,6 cm^-1
x = 1 cm
d (db) = 10 log (I/I0)
I /I0 = e ^-2 delta * x
I/I0 = e ^-1,2 = 0,30 ou 30 %
