Aula de 07/10 Física II

Apresentação de Eletricidade – materiais tipos

Parte deste material é voltado para estudo pessoal, e foi obtido pelo chatgpt.

Eletricidade: Eletricidade é o conjunto de fenômenos físicos associados à presença e ao fluxo de carga elétrica. Ela pode se manifestar de duas formas principais:

1. Eletricidade Estática: Refere-se à acumulação de cargas elétricas em um objeto, geralmente causada por atrito ou separação de materiais. Um exemplo clássico é quando você esfrega um balão em seu cabelo e ele fica “grudado” em uma parede.
2. Eletricidade Dinâmica ou Corrente Elétrica: É o fluxo ordenado de elétrons em um condutor, como um fio metálico.

Materiais Elétricos (do ponto de vista da física):

1. Condutores: São materiais que permitem o fluxo fácil de elétrons. Os metais, como o cobre, o ouro e a prata, são bons condutores. Eles possuem uma grande quantidade de elétrons livres que podem se mover facilmente através da estrutura do material.
2. Isolantes ou Dielétricos: São materiais que resistem ao fluxo de corrente elétrica. Exemplos comuns incluem borracha, vidro, e a maioria dos plásticos. Eles possuem poucos elétrons livres, tornando difícil para a corrente elétrica fluir através deles.
3. Semicondutores: São materiais cuja capacidade de conduzir eletricidade situa-se entre os condutores e os isolantes. O silício e o germânio são exemplos de semicondutores. Estes materiais são a base da moderna indústria de eletrônicos, mas do ponto de vista puramente físico, eles têm propriedades elétricas interessantes porque podem ser manipulados para alternar entre comportamento condutor e isolante.
4. Supercondutores: São materiais que, sob certas condições (geralmente temperaturas muito baixas), podem conduzir eletricidade sem qualquer resistência. Isso significa que, uma vez que uma corrente elétrica começa a fluir em um supercondutor, ela continuará indefinidamente até que algo seja feito para detê-la.
5. Materiais Ferromagnéticos: Embora não sejam classificados estritamente com base em suas propriedades elétricas, eles estão relacionados ao fenômeno elétrico por meio do magnetismo. Estes são materiais como o ferro e o níquel que podem ser facilmente magnetizados.

Material isolante

A física da eletricidade é fundamental para a compreensão de muitos aspectos do mundo moderno, desde a iluminação e aquecimento de nossas casas até a operação de dispositivos eletrônicos e comunicações. Essa é uma visão geral do tópico, e cada uma dessas categorias pode ser explorada em profundidade à medida que nos aprofundamos na física dos materiais e na teoria da eletricidade.

M

Para entender melhor o comportamento elétrico dos materiais, vamos começar examinando sua estrutura atômica:

Átomos e Cargas:
Todo átomo é composto por um núcleo (que contém prótons e nêutrons) e elétrons que orbitam o núcleo em camadas chamadas orbitais. Os prótons têm carga positiva, enquanto os elétrons têm carga negativa. Em condições normais, um átomo é neutro, o que significa que tem o mesmo número de prótons e elétrons, resultando em uma carga total de zero.

Tipos de Materiais e Suas Cargas:

1. Condutores:

• Os metais são bons condutores devido à presença de elétrons livres em sua estrutura.
• Em condutores, um ou mais elétrons de cada átomo estão desassociados do próprio átomo e movem-se livremente pelo material. São esses elétrons livres que permitem a condução de eletricidade.
• Quando uma diferença de potencial (tensão) é aplicada através de um condutor, os elétrons livres se movem em direção ao polo positivo, resultando em corrente elétrica.

1. Isolantes ou Dielétricos:

• Esses materiais têm uma estrutura atômica em que os elétrons estão fortemente ligados ao núcleo. Isso significa que há pouquíssimos ou nenhum elétron livre para se mover pelo material.
• Como resultado, os isolantes resistem ao fluxo de eletricidade e são usados para proteger e isolar os condutores.

1. Semicondutores:

• Os semicondutores, como silício e germânio, possuem propriedades elétricas intermediárias entre condutores e isolantes.
• A principal característica dos semicondutores é que sua condutividade pode ser alterada por diferentes métodos, como introdução de impurezas (dopagem) ou mudança de temperatura.
• Na dopagem, átomos de outros materiais são adicionados ao semicondutor para criar uma abundância de elétrons livres (dopagem tipo n) ou uma deficiência de elétrons, chamados de “buracos” (dopagem tipo p).

1. Supercondutores:

• Em certas condições, principalmente em temperaturas extremamente baixas, alguns materiais podem conduzir eletricidade sem resistência. Isso significa que não há perda de energia na forma de calor durante a condução.
• Essa ausência de resistência se deve a um fenômeno quântico em que os elétrons se movem em pares (pares de Cooper) sem colidir com átomos ou impurezas no material.

No contexto de cargas elétricas e movimento de cargas, a caracterização dos materiais como condutores, isolantes, semicondutores ou supercondutores é crucial. Essas categorias determinam como um material interage com a eletricidade e, portanto, quais aplicações são adequadas para cada tipo de material.

Lei de Coulomb

A Lei de Coulomb descreve a força eletrostática entre duas cargas puntiformes (ou seja, cargas que podem ser consideradas como pontos no espaço). Ela foi formulada pelo físico francês Charles-Augustin de Coulomb em 1785 e é fundamental para o estudo da eletrostática.

História:

Charles-Augustin de Coulomb, nascido em 1736, foi um engenheiro militar e físico francês. Através de seus experimentos precisos com uma balança de torção que ele mesmo inventou, Coulomb foi capaz de formular sua lei sobre a força eletrostática entre cargas. A balança de torção permitiu a ele medir forças muito pequenas entre cargas, e assim, ele pôde quantificar a relação entre a força eletrostática, a distância entre as cargas e a magnitude das cargas.

Princípio da Lei de Coulomb:

A Lei de Coulomb pode ser expressa matematicamente como:

Onde:

• ( F ) é a magnitude da força entre as duas cargas.
• ( q_1 ) e ( q_2 ) são as magnitudes das duas cargas.
• ( r ) é a distância entre o centro das duas cargas.
• ( k ) é a constante de proporcionalidade, conhecida como constante eletrostática. No vácuo, seu valor é aproximadamente :

Algumas observações sobre a Lei de Coulomb:

1. Natureza da Força: A força pode ser repulsiva ou atrativa, dependendo dos sinais das cargas. Se as cargas tiverem o mesmo sinal (ambas positivas ou ambas negativas), a força será repulsiva. Se tiverem sinais opostos, a força será atrativa.
2. Força Inversamente Proporcional ao Quadrado da Distância: A força eletrostática diminui com o quadrado da distância entre as cargas. Isso significa que, à medida que as cargas se afastam, a força entre elas diminui rapidamente.
3. Força Diretamente Proporcional ao Produto das Cargas: Se uma das cargas for dobrada, a força também dobrará. Se ambas as cargas forem dobradas, a força aumentará quatro vezes.

A Lei de Coulomb, junto com as leis do eletromagnetismo de Maxwell, forma a base para o entendimento moderno do eletromagnetismo.

Campo Eletrico

Campo Elétrico

Um campo elétrico é uma descrição do espaço ao redor de uma carga elétrica (ou um sistema de cargas elétricas) no qual outra carga experimentaria uma força elétrica devido à presença da primeira carga. Pode ser visualizado como uma “região de influência” em que a carga cria um efeito.

Definição:
O campo elétrico ( \mathbf{E} ) em um ponto no espaço é definido como a força elétrica ( \mathbf{F} ) que seria exercida sobre uma carga de prova positiva ( q_0 ) colocada naquele ponto, dividida pela magnitude da carga de prova:
[ \mathbf{E} = \frac{\mathbf{F}}{q_0} ]

Direção e Magnitude:

• A direção do campo elétrico em um ponto é a direção da força que uma carga positiva de prova sentiria se estivesse colocada naquele ponto.
• A magnitude do campo elétrico em um ponto é a força por unidade de carga que uma carga positiva de prova sentiria.

Propriedades:

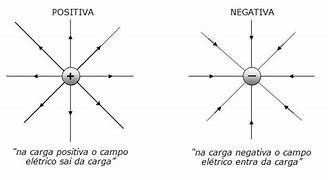
1. Fonte de Campo Elétrico: Uma carga positiva cria um campo elétrico que se irradia para fora dela, enquanto uma carga negativa cria um campo elétrico que se dirige para ela.
2. Superposição: Em uma região com várias cargas, o campo elétrico resultante em um ponto é a soma vetorial dos campos elétricos devidos a cada carga individual.
3. Unidades: No Sistema Internacional, o campo elétrico é medido em newtons por coulomb (N/C) ou, equivalentemente, em volts por metro (V/m).

Campo Elétrico Devido a uma Carga Pontual:
O campo elétrico devido a uma única carga pontual ( q ) é dado por:

onde:

• ( k ) é a constante eletrostática (aproximadamente ( 8.99 × 10^9 \, \text{N·m}^2/\text{C}^2 ) no vácuo).
• ( r ) é a distância do ponto de interesse à carga.

Linhas de Campo Elétrico:
As linhas de campo elétrico são uma representação gráfica usada para visualizar o campo elétrico. As regras para desenhar linhas de campo elétrico incluem:

• As linhas de campo originam-se em cargas positivas e terminam em cargas negativas.
• O número de linhas originadas ou terminadas em uma carga é proporcional à magnitude da carga.
• As linhas de campo são mais próximas onde o campo é mais forte e mais afastadas onde é mais fraco.

Efeitos:
Um campo elétrico pode fazer com que cargas se movam, podendo resultar em uma corrente elétrica se essas cargas estiverem em um condutor. Além disso, um campo elétrico pode induzir a polarização de materiais dielétricos, alinhando os dipolos elétricos do material com o campo.

A compreensão do conceito de campo elétrico é crucial para o entendimento de vários fenômenos elétricos e eletromagnéticos na física.

Lei de Gaus

A Lei de Gauss, nomeada em homenagem ao matemático e físico alemão Carl Friedrich Gauss, é uma das leis fundamentais da eletrostática e forma a base para muitos dos cálculos em eletromagnetismo. Ela fornece uma maneira de relacionar a distribuição de carga elétrica a seu campo elétrico resultante.

História:
Carl Friedrich Gauss (1777-1855) foi um dos matemáticos mais influentes da história. Embora seja mais conhecido por seu trabalho em matemática pura, ele também fez contribuições significativas à física. A Lei de Gauss foi primeiramente formulada por ele em 1813, mas foi publicada postumamente em 1867.

Princípios da Lei de Gauss:

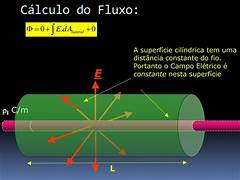
A Lei de Gauss afirma que o fluxo elétrico total através de uma superfície fechada é igual à carga total dentro dessa superfície dividida pela permissividade do vácuo. Matematicamente, ela é expressa como:
[ \oint \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{\text{int}}}{\varepsilon_0} ]

Onde:

• $$(\oint E\cdot dA)$$ representa o fluxo elétrico através da superfície, sendo ( \mathbf{E} ) o campo elétrico e $$\left(dA\right)$$ um elemento infinitesimal da superfície.
• $$\left(Q_{\text{int}}\right)$$ é a carga total dentro da superfície fechada.
• $$\left({\epsilon }_0\right)$$ é a permissividade do vácuo.

Aplicações e Implicações:

1. Simetria: A Lei de Gauss é particularmente útil em situações com alta simetria, como esferas, cilindros e placas planas. Em tais situações, pode-se simplificar cálculos do campo elétrico.
2. Condutores em Equilíbrio Eletrostático: Um resultado direto da Lei de Gauss é a constatação de que o campo elétrico dentro de um condutor em equilíbrio eletrostático é zero. Isso porque qualquer excesso de carga em um condutor se move para sua superfície.
3. Isolamento de Cargas: A Lei de Gauss pode ser usada para mostrar que qualquer carga dentro de um condutor fechado é completamente isolada do exterior. Isso é a base para o conceito de uma “gaiola de Faraday”.
4. Relação com a Lei de Coulomb: A Lei de Gauss pode ser derivada da Lei de Coulomb, mas, em muitos casos, é mais conveniente usar a Lei de Gauss para calcular campos elétricos, especialmente quando a simetria do problema é apropriada.

A Lei de Gauss, juntamente com as outras equações de Maxwell, fornece uma descrição completa dos fenômenos eletromagnéticos. É uma ferramenta poderosa em física, com aplicações em várias áreas, desde cálculos básicos de campo elétrico até avançadas teorias eletromagnéticas.

Potencial Elétrico

O potencial elétrico é uma quantidade escalar que descreve a capacidade de uma configuração elétrica (geralmente um campo elétrico) de realizar trabalho. É comumente usado para entender diferenças de energia em sistemas elétricos.

Definição:

O potencial elétrico ( V ) em um ponto no espaço é definido como o trabalho realizado pelo campo elétrico ao mover uma carga de prova positiva ( q_0 ) do infinito até esse ponto, dividido pela magnitude da carga de prova:

Unidades:
No Sistema Internacional, o potencial elétrico é medido em volts (V), onde 1 volt é equivalente a 1 joule por coulomb (J/C).

Princípios e Características:

1. Relação com Campo Elétrico: O campo elétrico ( \[\mathbf{E} \]) é relacionado à variação do potencial elétrico ( V ) pela relação:
   \[ \mathbf{E} = -\nabla V \]
   onde ( \nabla V ) é o gradiente do potencial. Essa relação nos diz que o campo elétrico aponta na direção da maior variação do potencial elétrico e tem magnitude igual ao declive máximo do potencial.
2. Potencial devido a uma Carga Pontual: O potencial elétrico ( V ) devido a uma carga pontual ( q ) a uma distância ( r ) é dado por:
   \[ V = \frac{kq}{r} \]
   onde ( k ) é a constante eletrostática.
3. Superposição: Em uma região com várias cargas, o potencial elétrico em um ponto é a soma dos potenciais devidos a cada carga individual. Isso é uma consequência do princípio da superposição.
4. Equipotenciais: Superfícies equipotenciais são locais onde o potencial elétrico tem o mesmo valor. Não há fluxo de corrente elétrica ao longo de uma superfície equipotencial porque não há diferença de potencial.
5. Trabalho: O trabalho realizado pelo campo elétrico ao mover uma carga ( q ) entre dois pontos com potenciais ( V_A ) e ( V_B ) é:
   \[ W = q(V_B – V_A) \]
6. Potencial Elétrico e Energia Potencial: A energia potencial elétrica ( U ) associada a uma carga ( q ) em um ponto onde o potencial elétrico é ( V ) é:
   \[ U = qV \]

Aplicações:
O conceito de potencial elétrico é fundamental em circuitos elétricos, especialmente quando se trata de componentes como capacitores. Também é essencial na análise de campos elétricos em configurações complexas e na compreensão da diferença de potencial (tensão) em dispositivos elétricos.

Capacitância Elétrica

A capacitância é uma propriedade dos sistemas que permite o armazenamento de energia na forma de um campo elétrico. Os dispositivos projetados para terem uma capacitância específica e utilizados para armazenar e liberar energia elétrica são chamados de capacitores.

Definição:

A capacitância ( C ) de um dispositivo é definida como a razão entre a carga ( Q ) armazenada nele e o potencial elétrico ( V ) ou diferença de potencial (tensão) através dele:
\[ C = \frac{Q}{V} \]

Unidades:
No Sistema Internacional, a unidade de capacitância é o farad (F), onde 1 farad é equivalente a 1 coulomb por volt (C/V).

Princípios e Características:

1. Capacitância e Geometria: A capacitância de um capacitor é geralmente determinada pela geometria do dispositivo (como a área das placas e a distância entre elas, no caso de um capacitor de placas paralelas) e pelo material dielétrico (ou isolante) presente entre as placas.
2. Capacitor de Placas Paralelas: Para um capacitor formado por duas placas paralelas com área ( A ) separadas por uma distância ( d ) e preenchidas com um dielétrico de permissividade ( \varepsilon ), a capacitância é dada por:
   \[C = \frac{\varepsilon A}{d} \]
3. Armazenamento de Energia: A energia ( U ) armazenada em um capacitor carregado é dada por:
   \[ U = \frac{1}{2} C V^2 \]
4. Capacitores em Série e Paralelo:

• Quando capacitores são conectados em série, a capacitância equivalente ( C_{eq} ) é dada por:
  \[ \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \ldots \]
• Quando capacitores são conectados em paralelo, a capacitância equivalente ( C_{eq} ) é a soma das capacitâncias individuais:
  \[ C_{eq} = C_1 + C_2 + \ldots \]

1. Dielétricos: A inserção de um dielétrico entre as placas de um capacitor aumenta sua capacitância. O dielétrico é caracterizado por sua constante dielétrica \[( \kappa )\], e a permissividade do dielétrico é \[( \varepsilon = \kappa \varepsilon_0 )\], onde \[( \varepsilon_0 )\] é a permissividade do vácuo.

Aplicações:
Capacitores são componentes essenciais em circuitos eletrônicos. Eles são usados para:

• Armazenar e liberar energia (como em flashes de câmeras).
• Filtrar ruído ou regular a tensão em fontes de alimentação.
• Criar osciladores em circuitos de rádio e televisão.
• Definir tempos de resposta em circuitos temporizadores.

Em sistemas de potência, os capacitores também são usados para corrigir o fator de potência de redes elétricas.

Densidade de Corrente Elétrica

A densidade de corrente elétrica é uma quantidade vetorial que descreve o fluxo de carga elétrica por unidade de área através de um material. Ela é uma medida da quantidade de corrente que passa por uma seção transversal de um material.

Definição:

A densidade de corrente elétrica $$\left(J\right)$$ é definida como a corrente ( I ) por unidade de área ( A ) perpendicular ao fluxo da corrente:
$$J=\frac{I}{A}$$

Direção:
A direção da densidade de corrente é a direção do fluxo de carga positiva. Em metais, a corrente elétrica é devida ao movimento de elétrons (que são cargas negativas), então a densidade de corrente tem a direção oposta ao movimento dos elétrons.

Unidades:
No Sistema Internacional, a unidade de densidade de corrente é o ampère por metro quadrado $$\left(A/m^2\right)$$.

Relação com a Condutividade:

A densidade de corrente pode também ser relacionada com o campo elétrico $$\left(E\right)$$ e a condutividade ( \sigma ) do material pela lei de Ohm no formato diferencial:
$$J=\sigma E$$

Aqui, ( \sigma ) é a condutividade do material (o inverso da resistividade) e ( \mathbf{E} ) é o campo elétrico no material.

Fatores que Afetam a Densidade de Corrente:

1. Material: Diferentes materiais têm diferentes números de portadores de carga livres. Por exemplo, metais têm uma alta densidade de elétrons livres, levando a altas densidades de corrente sob a aplicação de um campo elétrico.
2. Temperatura: A densidade de corrente pode também ser influenciada pela temperatura. Em alguns materiais, o aumento da temperatura pode aumentar a resistividade, diminuindo a densidade de corrente. Em supercondutores, abaixo de uma temperatura crítica, a resistividade se torna zero, permitindo uma densidade de corrente muito alta.
3. Campo Elétrico Aplicado: Em muitos materiais, a densidade de corrente é diretamente proporcional ao campo elétrico aplicado, conforme expresso pela relação mencionada com a condutividade.

Importância e Aplicações:
A densidade de corrente é um conceito crucial em eletrônica e eletromagnetismo. Ela é fundamental no design e análise de dispositivos eletrônicos, no estudo de materiais supercondutores, na descrição de efeitos térmicos em condutores, e em muitas outras áreas da ciência e engenharia.

A resistência elétrica de um condutor pode ser calculada em função da resistividade elétrica do material, juntamente com as dimensões físicas do condutor.

A relação é dada pela seguinte fórmula:

\[ R = \rho \frac{L}{A} \]

Onde:

• ( R ) é a resistência do condutor.
• $$\left(\rho \right)$$ (rho) é a resistividade elétrica do material (medida em ohm-metro, ( \Omega \cdot m )).
• ( L ) é o comprimento do condutor (medido em metros, ( m )).
• ( A ) é a área da seção transversal do condutor (medida em metros quadrados, \[( m^2 ))\].

Explicação:

A resistividade é uma propriedade intrínseca do material, representando a resistência ao fluxo de corrente elétrica. Materiais com alta resistividade (como borracha ou vidro) são geralmente isolantes, enquanto materiais com baixa resistividade (como cobre ou alumínio) são condutores.

• Comprimento ( L ): Quanto maior o comprimento de um condutor, maior será a resistência, pois os elétrons têm um caminho mais longo para percorrer, aumentando a probabilidade de colisões e, consequentemente, a resistência.
• Área da seção transversal ( A ): Quanto maior a área da seção transversal de um condutor, menor será a resistência. Isso porque um condutor mais amplo permite que mais elétrons passem por ele simultaneamente.

Então, para encontrar a resistência de um condutor com base em sua resistividade, você precisará conhecer as dimensões físicas do condutor e a resistividade do material do qual ele é feito. Usando a fórmula acima, você pode determinar a resistência desse condutor.