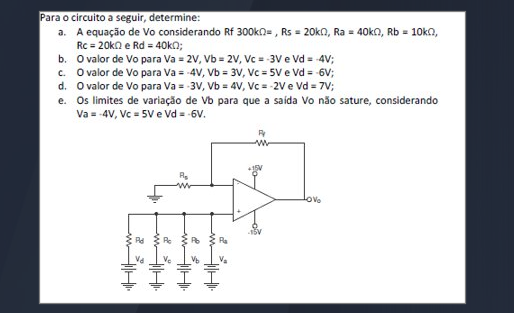
Circuit Calculations

a) Equação de V_o

Para encontrar a equação de V_o em função das tensões de entrada V_a, V_b, V_c, V_d, aplicamos a superposição das contribuições de cada tensão de entrada no amplificador operacional. A equação geral para um somador inversor é dada por:

V_o = – ( (R_f/R_a) V_a + (R_f/R_b) V_b + (R_f/R_c) V_c + (R_f/R_d) V_d )

Dado:

• R_f = 300 kΩ
• R_s = 20 kΩ
• R_a = 40 kΩ
• R_b = 10 kΩ
• R_c = 20 kΩ
• R_d = 40 kΩ

Podemos escrever a equação de V_o como:

V_o = – ( (300 kΩ/40 kΩ) V_a + (300 kΩ/10 kΩ) V_b + (300 kΩ/20 kΩ) V_c + (300 kΩ/40 kΩ) V_d )

V_o = – ( 7.5 V_a + 30 V_b + 15 V_c + 7.5 V_d )

b) Valor de V_o para V_a = 2V, V_b = 2V, V_c = 3V, V_d = -4V

Substituindo os valores na equação encontrada:

V_o = – ( 7.5 * 2 + 30 * 2 + 15 * 3 + 7.5 * (-4) )

V_o = – ( 15 + 60 + 45 – 30 )

V_o = – ( 90 )

V_o = -90V

c) Valor de V_o para V_a = -4V, V_b = 3V, V_c = 5V, V_d = -6V

Substituindo os valores na equação encontrada:

V_o = – ( 7.5 * (-4) + 30 * 3 + 15 * 5 + 7.5 * (-6) )

V_o = – ( -30 + 90 + 75 – 45 )

V_o = – ( 90 )

V_o = -90V

d) Valor de V_o para V_a = -3V, V_b = 4V, V_c = -2V, V_d = 7V

Substituindo os valores na equação encontrada:

V_o = – ( 7.5 * (-3) + 30 * 4 + 15 * (-2) + 7.5 * 7 )

V_o = – ( -22.5 + 120 – 30 + 52.5 )

V_o = – ( 120 )

V_o = -120V

e) Limites de variação de V_b para que a saída V_o não sature, considerando V_a = -4V, V_c = 5V e V_d = -6V

Para que V_o não sature, precisamos garantir que V_o fique dentro da faixa de alimentação do amplificador operacional, que geralmente é de ±15V.

Substituindo V_a, V_c e V_d na equação e isolando V_b:

V_o = – ( 7.5 * (-4) + 30 * V_b + 15 * 5 + 7.5 * (-6) )

Simplificando:

V_o = – ( -30 + 30 V_b + 75 – 45 )

V_o = – ( 30 V_b )

Como V_o deve estar entre -15V e +15V:

-15V ≤ – ( 30 V_b ) ≤ 15V

-15V ≤ – 30 V_b ≤ 15V

– (15V/30) ≤ V_b ≤ (15V/30)

-0.5V ≤ V_b ≤ 0.5V

Então, V_b deve variar entre -0.5V e 0.5V para que a saída V_o não sature.

Exercício 2

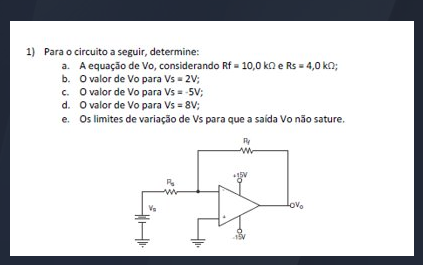
a) Equação de V_o

Para encontrar a equação de V_o considerando R_f = 10,0 kΩ e R_s = 4,0 kΩ, usamos a fórmula do amplificador inversor:

V_o = – ( (R_f/R_s) V_s )

Dado:

• R_f = 10,0 kΩ
• R_s = 4,0 kΩ

Portanto, a equação de V_o é:

V_o = – ( 10,0 kΩ / 4,0 kΩ ) V_s

V_o = – ( 2.5 V_s )

b) Valor de V_o para V_s = 2V

Substituindo V_s = 2V na equação encontrada:

V_o = – ( 2.5 * 2 )

V_o = – 5V

c) Valor de V_o para V_s = 5V

Substituindo V_s = 5V na equação encontrada:

V_o = – ( 2.5 * 5 )

V_o = – 12.5V

d) Valor de V_o para V_s = 8V

Substituindo V_s = 8V na equação encontrada:

V_o = – ( 2.5 * 8 )

V_o = – 20V

e) Limites de variação de V_s para que a saída V_o não sature

Para que V_o não sature, precisamos garantir que V_o fique dentro da faixa de alimentação do amplificador operacional, que geralmente é de ±15V.

Usando a equação V_o = -2.5 V_s:

-15V ≤ -2.5 V_s ≤ 15V

Dividindo todos os termos por -2.5 (e invertendo a desigualdade):

6V ≥ V_s ≥ -6V

Então, V_s deve variar entre -6V e 6V para que a saída V_o não sature.

Exercício 3

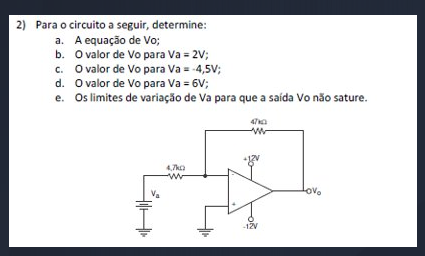
a) Equação de V_o

Para encontrar a equação de V_o considerando um amplificador inversor com os resistores R_f e R_s, usamos a fórmula do amplificador inversor:

V_o = – ( (R_f/R_s) V_a )

Dado:

• R_f = 47 kΩ
• R_s = 4,7 kΩ

Portanto, a equação de V_o é:

V_o = – ( 47 kΩ / 4,7 kΩ ) V_a

V_o = – ( 10 V_a )

b) Valor de V_o para V_a = 2V

Substituindo V_a = 2V na equação encontrada:

V_o = – ( 10 * 2 )

V_o = – 20V

c) Valor de V_o para V_a = -4,5V

Substituindo V_a = -4,5V na equação encontrada:

V_o = – ( 10 * -4,5 )

V_o = 45V

d) Valor de V_o para V_a = 6V

Substituindo V_a = 6V na equação encontrada:

V_o = – ( 10 * 6 )

V_o = – 60V

e) Limites de variação de V_a para que a saída V_o não sature

Para que V_o não sature, precisamos garantir que V_o fique dentro da faixa de alimentação do amplificador operacional, que geralmente é de ±12V.

Usando a equação V_o = -10 V_a:

-12V ≤ -10 V_a ≤ 12V

Dividindo todos os termos por -10 (e invertendo a desigualdade):

1.2V ≥ V_a ≥ -1.2V

Então, V_a deve variar entre -1.2V e 1.2V para que a saída V_o não sature.

Exercício 4

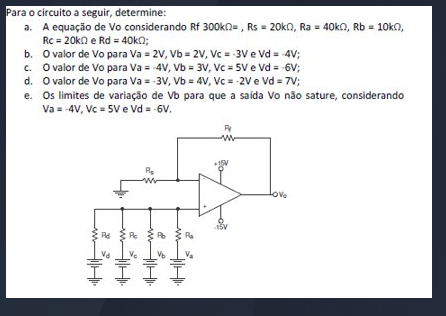
a) Equação de V_o

Para encontrar a equação de V_o considerando um amplificador inversor com os resistores R_f e R_s, usamos a fórmula do amplificador inversor:

V_o = – ( (R_f/R_s) V_a )

Dado:

• R_f = 47 kΩ
• R_s = 4,7 kΩ

Portanto, a equação de V_o é:

V_o = – ( 47 kΩ / 4,7 kΩ ) V_a

V_o = – ( 10 V_a )

b) Valor de V_o para V_a = 2V

Substituindo V_a = 2V na equação encontrada:

V_o = – ( 10 * 2 )

V_o = – 20V

c) Valor de V_o para V_a = -4,5V

Substituindo V_a = -4,5V na equação encontrada:

V_o = – ( 10 * -4,5 )

V_o = 45V

d) Valor de V_o para V_a = 6V

Substituindo V_a = 6V na equação encontrada:

V_o = – ( 10 * 6 )

V_o = – 60V

e) Limites de variação de V_a para que a saída V_o não sature

Para que V_o não sature, precisamos garantir que V_o fique dentro da faixa de alimentação do amplificador operacional, que geralmente é de ±12V.

Usando a equação V_o = -10 V_a:

-12V ≤ -10 V_a ≤ 12V

Dividindo todos os termos por -10 (e invertendo a desigualdade):

1.2V ≥ V_a ≥ -1.2V

Então, V_a deve variar entre -1.2V e 1.2V para que a saída V_o não sature.