Fundamentos da Estatística Descritiva – Média, Mediana, Moda e Desvio Padrão

A estatística descritiva é fundamental para analisar dados e identificar padrões. Neste artigo, vamos explorar quatro conceitos essenciais: média, mediana, moda e desvio padrão. Eles são ferramentas básicas, mas poderosas, para descrever e interpretar conjuntos de dados.

1. Média

A média, também conhecida como média aritmética, é o valor típico de um conjunto de dados. Ela é calculada somando todos os valores e dividindo pelo número de valores. A média representa um “centro” dos dados, mas é sensível a valores extremos.

Fórmula:

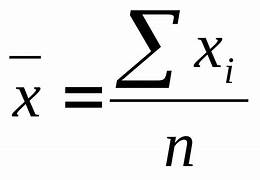
Onde:

• ∑xi é a soma de todos os valores.
• n é o número total de valores.

Vou gerar uma imagem ilustrando um conjunto de dados e a média.

Como fazer em python:

import statistics

# Dados de exemplo
dados = [10, 20, 30, 40, 50]

# Calculando a média
media = statistics.mean(dados)
print("Média:", media)

2. Mediana

A mediana é o valor central em um conjunto de dados ordenado. Ela é útil quando o conjunto tem valores extremos, pois não é influenciada por esses valores, ao contrário da média.

• Se o número de valores é ímpar, a mediana é o valor do meio.
• Se o número de valores é par, a mediana é a média dos dois valores centrais.

Exemplo: Em {3, 5, 7, 9, 11}, a mediana é 7, o valor do meio.

Vou criar uma imagem para mostrar como encontrar a mediana em conjuntos com números ímpares e pares de dados.

Em python:

# Dados de exemplo
dados = [10, 20, 30, 40, 50]
dados.sort()  # Ordenar os dados

n = len(dados)
if n % 2 == 1:
    # Número ímpar de elementos
    mediana = dados[n // 2]
else:
    # Número par de elementos
    mediana = (dados[n // 2 - 1] + dados[n // 2]) / 2

print("Mediana:", mediana)

3. Moda

A moda é o valor que mais aparece em um conjunto de dados. Ao contrário da média e da mediana, a moda representa a frequência.

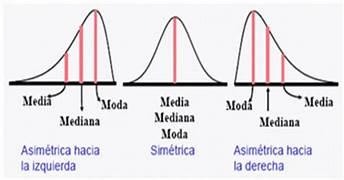
Exemplo: Em {3, 3, 4, 5, 6}, a moda é 3, pois aparece mais vezes.

Gero uma imagem mostrando um conjunto de dados com a moda destacada.

Em python:

import statistics

# Dados de exemplo com valores repetidos
dados = [10, 20, 20, 30, 40, 40, 40, 50]

# Calculando a moda
moda = statistics.mode(dados)
print("Moda:", moda)

Gerando o gráfico em python

import matplotlib.pyplot as plt
from collections import Counter

# Dados de exemplo com valores repetidos
dados = [10, 20, 20, 30, 40, 40, 40, 50]

# Contando a frequência de cada valor
frequencia = Counter(dados)
valores = list(frequencia.keys())
contagens = list(frequencia.values())

# Encontrando a moda
moda = max(frequencia, key=frequencia.get)
moda_frequencia = frequencia[moda]

# Criando o gráfico de barras
plt.figure(figsize=(8, 6))
plt.bar(valores, contagens, color='skyblue')
plt.xlabel('Valores')
plt.ylabel('Frequência')
plt.title('Gráfico de Frequência - Moda')
plt.axhline(moda_frequencia, color='red', linestyle='--', label=f'Moda = {moda}')
plt.legend()

plt.show()

Mostrando o gráfico:

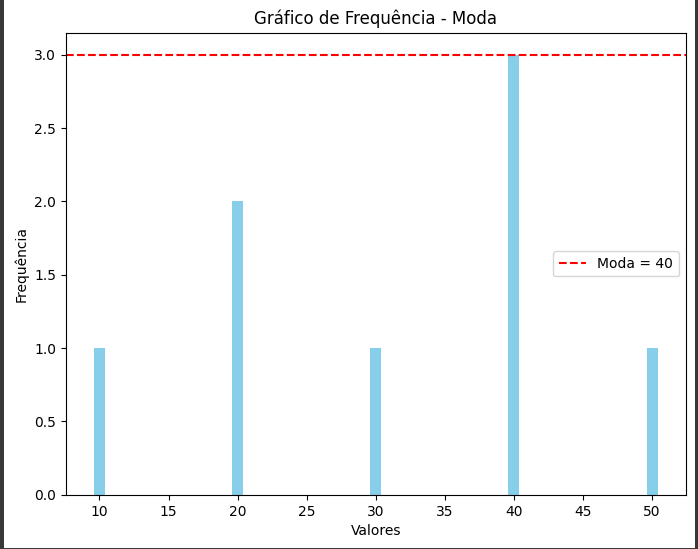
4. Desvio Padrão

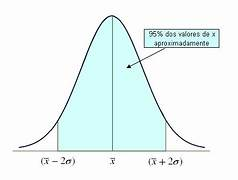
O desvio padrão mede a dispersão dos dados em relação à média. Ele indica o quão próximos ou dispersos os valores estão em relação ao valor médio.

Um desvio padrão baixo significa que os valores estão próximos da média, enquanto um desvio alto indica maior variabilidade.

Gerando em python:

import statistics

# Dados de exemplo
dados = [10, 20, 30, 40, 50]

# Calculando o desvio padrão
desvio_padrao = statistics.stdev(dados)
print("Desvio Padrão:", desvio_padrao)