Métodos de Busca
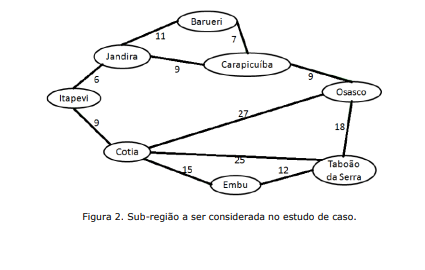
3 de outubro de 2021Assim, considerando o grafo da Figura 2, que representa a sub-região circulada na Figura 1, e a tabela heurística da Figura 3, represente o problema (Estado, S, s0, G, A e Matriz de Adjacências) e apresente soluções (caminho e custo em Km) para o problema descrito utilizando os seguintes algoritmos de busca: Menor Custo, Dijkstra (árvore), Melhor Estimativa e A*.
Observação: Para referenciar uma cidade use apenas as três primeiras letras.
Exercício
Usar método de menor custo de Itapevi até Osasco.
Tabela de distância até Osasco em linha reta
| Cidade | Distância KM |
| Barueri | 12 |
| Carapicuíba | 6 |
| Cotia | 17 |
| Embú | 15 |
| Itapevi | 23 |
| Jandira | 18 |
| Osasco | 0 |
| Taboão da Serra | 8 |
Estimativa de distância até Osasco
Diagrama de conexões
Árvore de busca de menor custo Itapevi/Osasco
Nesta arvore usamos o custo associado de deslocamento, fazendo todas as conexões possíveis.
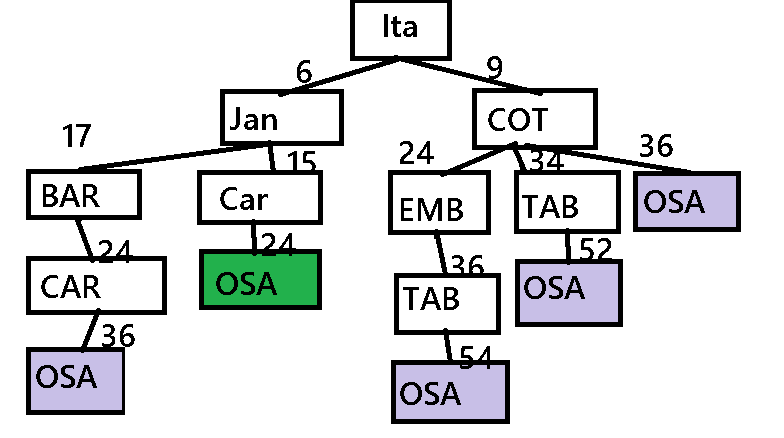
Ficando definido a melhor rota Itapevi/Jandira/Carapicuíba/Osasco.
Árvore Dijkstra
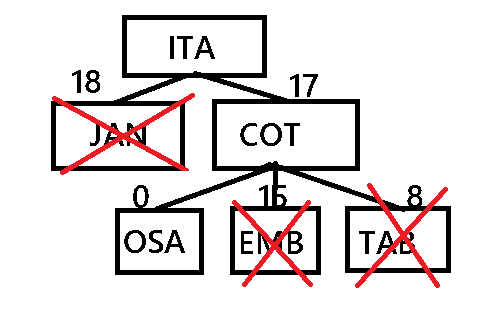
Nesta arvore usamos o custo, associado a podas, ignorando os métodos que tem maior custo.
Este método tem podas em Carapicuíba (26) Taboão (36), conforme figura abaixo:

Ficando definido a melhor rota Itapevi/Jandira/Carapicuíba/Osasco.
Árvore Melhor Estimativa
Neste método, usamos a distância até Osasco, pegando sempre a menor distância e ignorando as demais.
Árvore A*
Nesta arvore somamos o custo a distância, criando um valor ficticio. Que será a base da poda.
É uma arvore heuristica, ou seja toma decisões.
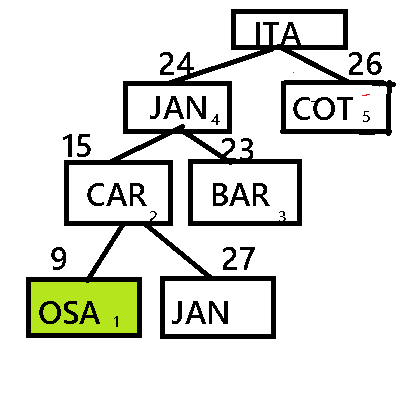
Neste método somamos os valores.
Sendo:
JAN(4) = 6+18
COT(4)= 8+17
BAR(3) 11+12
CAR(2) 9+6
OSA(1) 9+0
JAN(6) 9+18
