Prof. Raphael Pinheiro

Link do trabalho:

https://github.com/raphaelPinheiro26/Processamento-de-Sinais-e-Imagens—Fatec-RP/blob/main/Processamento_Estat%C3%ADstico_e_Convolu%C3%A7%C3%A3o.ipynb

Alunos:

Marcelo Maurin Martins

Lorena Froes

Exercício 1

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import curve_fit

# Função para criar a distribuição gaussiana aleatória
def create_gaussian_distribution(mean=0, stddev=1, num_samples=1000):
    return np.random.normal(mean, stddev, num_samples)

# Função gaussiana para ajuste
def gaussian(x, amplitude, mean, stddev):
    return amplitude * np.exp(-((x - mean) ** 2) / (2 * stddev ** 2))

# Função para calcular o FWHM
def calculate_fwhm(data):
    # Histograma dos dados
    counts, bin_edges = np.histogram(data, bins=100, density=True)
    bin_centers = (bin_edges[:-1] + bin_edges[1:]) / 2

    # Ajuste da curva gaussiana
    popt, _ = curve_fit(gaussian, bin_centers, counts, p0=[1, np.mean(data), np.std(data)])
    amplitude, mean, stddev = popt

    # FWHM para uma distribuição gaussiana é 2 * sqrt(2 * ln(2)) * stddev
    fwhm = 2 * np.sqrt(2 * np.log(2)) * stddev

    # Plot para visualização (opcional)
    plt.hist(data, bins=100, density=True, alpha=0.6, color='g')
    plt.plot(bin_centers, gaussian(bin_centers, *popt), linewidth=2, color='r')
    plt.title(f'Gaussian Fit: Mean = {mean:.2f}, Stddev = {stddev:.2f}, FWHM = {fwhm:.2f}')
    plt.xlabel('Value')
    plt.ylabel('Probability Density')
    plt.show()

    return fwhm

# Exemplo de uso
data = create_gaussian_distribution(mean=0, stddev=1, num_samples=1000)
fwhm = calculate_fwhm(data)
print(f'FWHM: {fwhm}')

Exercício 2

Descreva plote os gráficos a seguir:

Uso de Parenthesis: x(t) = y(t)

import numpy as np
import matplotlib.pyplot as plt

# Definir o intervalo de tempo
t = np.linspace(0, 10, 1000)

# Definir as funções x(t) e y(t)
x_t = np.sin(2 * np.pi * t)
y_t = np.cos(2 * np.pi * t)

# Criar o gráfico
plt.figure(figsize=(10, 6))

plt.plot(t, x_t, label='$x(t) = \sin(2\pi t)$', color='b')
plt.plot(t, y_t, label='$y(t) = \cos(2\pi t)$', color='r')

plt.title('Sinal Contínuo: $x(t)$ e $y(t)$')
plt.xlabel('Tempo $t$')
plt.ylabel('Amplitude')
plt.legend()
plt.grid(True)

plt.show()

Após executar a função, temos o gráfico

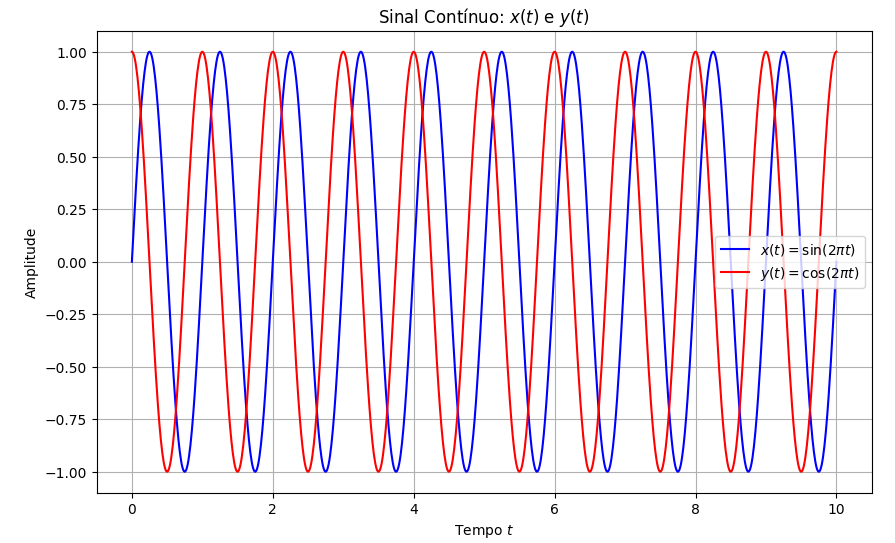
Agora iremos mostrar o gráfico x[t], y[t]:

Onde o mesmo é uma apresentação de um sinal discreto, ou seja , ele apresenta de forma não contínua. Sendo taxas de amostragem ao longo do tempo.

import numpy as np
import matplotlib.pyplot as plt

# Definir o intervalo de tempo contínuo
t_continuous = np.linspace(0, 10, 1000)

# Definir o intervalo de tempo discreto
t_discrete = np.arange(0, 10, 0.1)

# Definir as funções contínuas x(t) e y(t)
x_t_continuous = np.sin(2 * np.pi * t_continuous)
y_t_continuous = np.cos(2 * np.pi * t_continuous)

# Definir as funções discretas x[t] e y[t]
x_t_discrete = np.sin(2 * np.pi * t_discrete)
y_t_discrete = np.cos(2 * np.pi * t_discrete)

# Criar os gráficos
fig, axs = plt.subplots(2, 1, figsize=(10, 12))

# Gráfico do sinal contínuo
axs[0].plot(t_continuous, x_t_continuous, label='$x(t) = \sin(2\pi t)$', color='b')
axs[0].plot(t_continuous, y_t_continuous, label='$y(t) = \cos(2\pi t)$', color='r')
axs[0].set_title('Sinal Contínuo: $x(t)$ e $y(t)$')
axs[0].set_xlabel('Tempo $t$')
axs[0].set_ylabel('Amplitude')
axs[0].legend()
axs[0].grid(True)

# Gráfico do sinal discreto
axs[1].stem(t_discrete, x_t_discrete, label='$x[t] = \sin(2\pi t)$', linefmt='b-', markerfmt='bo', basefmt='r-')
axs[1].stem(t_discrete, y_t_discrete, label='$y[t] = \cos(2\pi t)$', linefmt='r-', markerfmt='ro', basefmt='r-')
axs[1].set_title('Sinal Discreto: $x[t]$ e $y[t]$')
axs[1].set_xlabel('Tempo $t$')
axs[1].set_ylabel('Amplitude')
axs[1].legend()
axs[1].grid(True)

plt.tight_layout()
plt.show()

Ficando conforme apresentado a seguir:

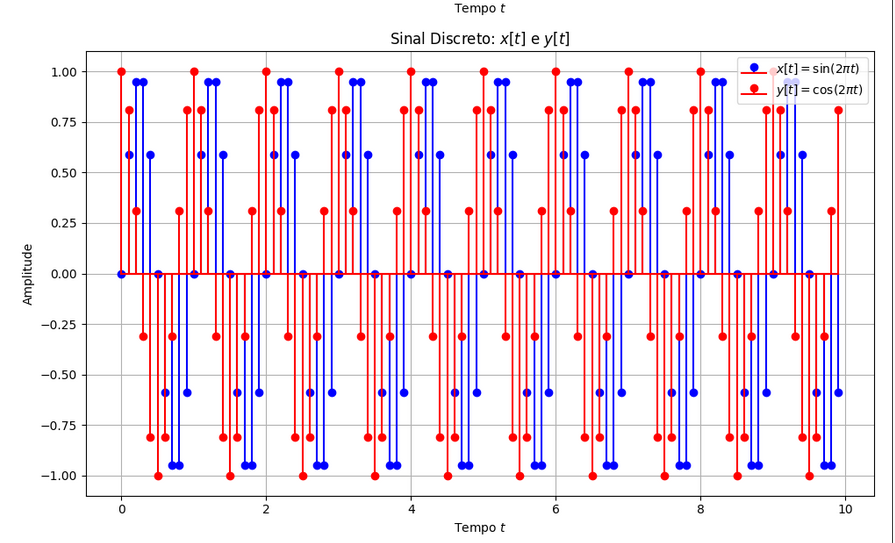
expressão x[n] -> system-> y[n]

import numpy as np
import matplotlib.pyplot as plt

# Definir o intervalo de tempo discreto
n = np.arange(0, 20, 1)

# Definir a função de entrada x[n]
x_n = np.sin(2 * np.pi * n / 10)

# Definir a constante de escala k
k = 2

# Aplicar o sistema para obter a saída y[n]
y_n = k * x_n

# Criar os gráficos
fig, axs = plt.subplots(2, 1, figsize=(10, 8))

# Gráfico do sinal de entrada x[n]
axs[0].stem(n, x_n, label='$x[n] = \sin(2\pi n / 10)$', linefmt='b-', markerfmt='bo', basefmt='r-')
axs[0].set_title('Sinal de Entrada: $x[n]$')
axs[0].set_xlabel('n')
axs[0].set_ylabel('Amplitude')
axs[0].legend()
axs[0].grid(True)

# Gráfico do sinal de saída y[n]
axs[1].stem(n, y_n, label='$y[n] = 2 \cdot x[n]$', linefmt='r-', markerfmt='ro', basefmt='r-')
axs[1].set_title('Sinal de Saída: $y[n]$')
axs[1].set_xlabel('n')
axs[1].set_ylabel('Amplitude')
axs[1].legend()
axs[1].grid(True)

plt.tight_layout()
plt.show()

Homogenidade, x[n] -> system-> y[n]; No exemplo expresso pela função: y[n]=k⋅x[n]

import numpy as np
import matplotlib.pyplot as plt

# Definir o intervalo de tempo discreto
n = np.arange(0, 20, 1)

# Definir a função de entrada x[n]
x_n = np.sin(2 * np.pi * n / 10)

# Definir a constante de escala k
k = 2

# Aplicar o sistema para obter a saída y[n]
y_n = k * x_n

# Criar os gráficos
fig, axs = plt.subplots(2, 1, figsize=(10, 8))

# Gráfico do sinal de entrada x[n]
axs[0].stem(n, x_n, label='$x[n] = \sin(2\pi n / 10)$', linefmt='b-', markerfmt='bo', basefmt='r-')
axs[0].set_title('Sinal de Entrada: $x[n]$')
axs[0].set_xlabel('n')
axs[0].set_ylabel('Amplitude')
axs[0].legend()
axs[0].grid(True)

# Gráfico do sinal de saída y[n]
axs[1].stem(n, y_n, label='$y[n] = 2 \cdot x[n]$', linefmt='r-', markerfmt='ro', basefmt='r-')
axs[1].set_title('Sinal de Saída: $y[n]$')
axs[1].set_xlabel('n')
axs[1].set_ylabel('Amplitude')
axs[1].legend()
axs[1].grid(True)

plt.tight_layout()
plt.show()

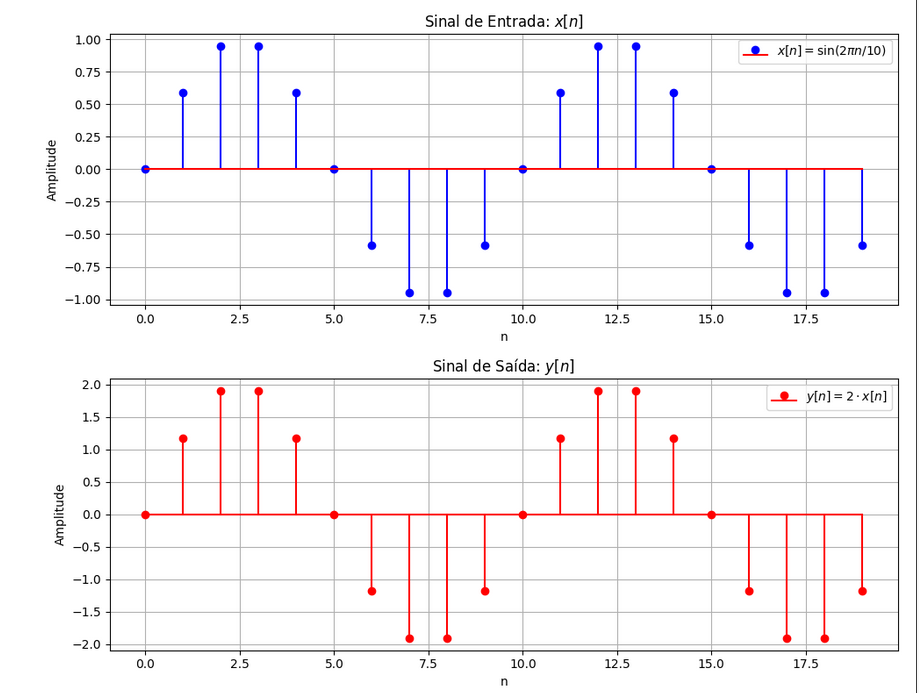
agora de aditivo, tal como x1[n]+x2[n] -> system -> y1[n] + y2[n], tal como um exemplo, podemos apresentar o exemplo de um ruído.

import numpy as np
import matplotlib.pyplot as plt

# Definir o intervalo de tempo discreto
n = np.arange(0, 20, 1)

# Definir as funções de entrada x1[n] e x2[n]
x1_n = np.sin(2 * np.pi * n / 10)
x2_n = np.cos(2 * np.pi * n / 10)

# Definir a constante de escala k
k = 2

# Aplicar o sistema para obter as saídas y1[n] e y2[n]
y1_n = k * x1_n
y2_n = k * x2_n

# Aplicar o sistema para a soma das entradas
x_sum_n = x1_n + x2_n
y_sum_n = k * x_sum_n

# Calcular a soma das saídas individuais
y_sum_individual_n = y1_n + y2_n

# Criar os gráficos
fig, axs = plt.subplots(3, 1, figsize=(10, 12))

# Gráfico dos sinais de entrada x1[n] e x2[n]
axs[0].stem(n, x1_n, label='$x_1[n] = \sin(2\pi n / 10)$', linefmt='b-', markerfmt='bo', basefmt='r-')
axs[0].stem(n, x2_n, label='$x_2[n] = \cos(2\pi n / 10)$', linefmt='g-', markerfmt='go', basefmt='r-')
axs[0].set_title('Sinais de Entrada: $x_1[n]$ e $x_2[n]$')
axs[0].set_xlabel('n')
axs[0].set_ylabel('Amplitude')
axs[0].legend()
axs[0].grid(True)

# Gráfico dos sinais de saída y1[n] e y2[n]
axs[1].stem(n, y1_n, label='$y_1[n] = 2 \cdot x_1[n]$', linefmt='b-', markerfmt='bo', basefmt='r-')
axs[1].stem(n, y2_n, label='$y_2[n] = 2 \cdot x_2[n]$', linefmt='g-', markerfmt='go', basefmt='r-')
axs[1].set_title('Sinais de Saída: $y_1[n]$ e $y_2[n]$')
axs[1].set_xlabel('n')
axs[1].set_ylabel('Amplitude')
axs[1].legend()
axs[1].grid(True)

# Gráfico da soma das saídas comparado à saída da soma das entradas
axs[2].stem(n, y_sum_n, label='$y[n] = 2 \cdot (x_1[n] + x_2[n])$', linefmt='r-', markerfmt='ro', basefmt='r-')
axs[2].stem(n, y_sum_individual_n, label='$y_1[n] + y_2[n]$', linefmt='m-', markerfmt='mo', basefmt='r-')
axs[2].set_title('Comparação: $y[n]$ e $y_1[n] + y_2[n]$')
axs[2].set_xlabel('n')
axs[2].set_ylabel('Amplitude')
axs[2].legend()
axs[2].grid(True)

plt.tight_layout()
plt.show()

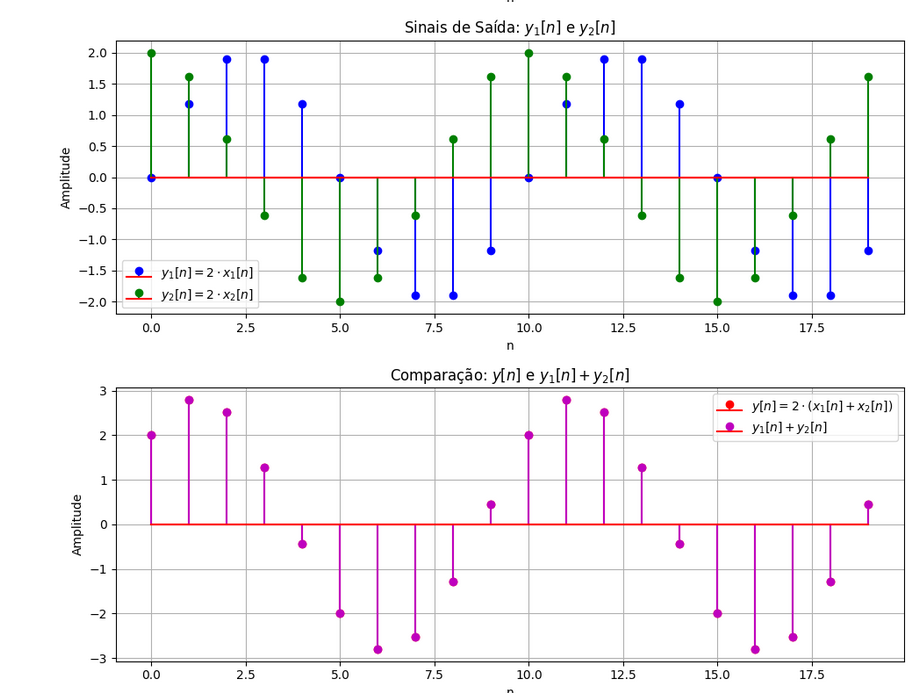
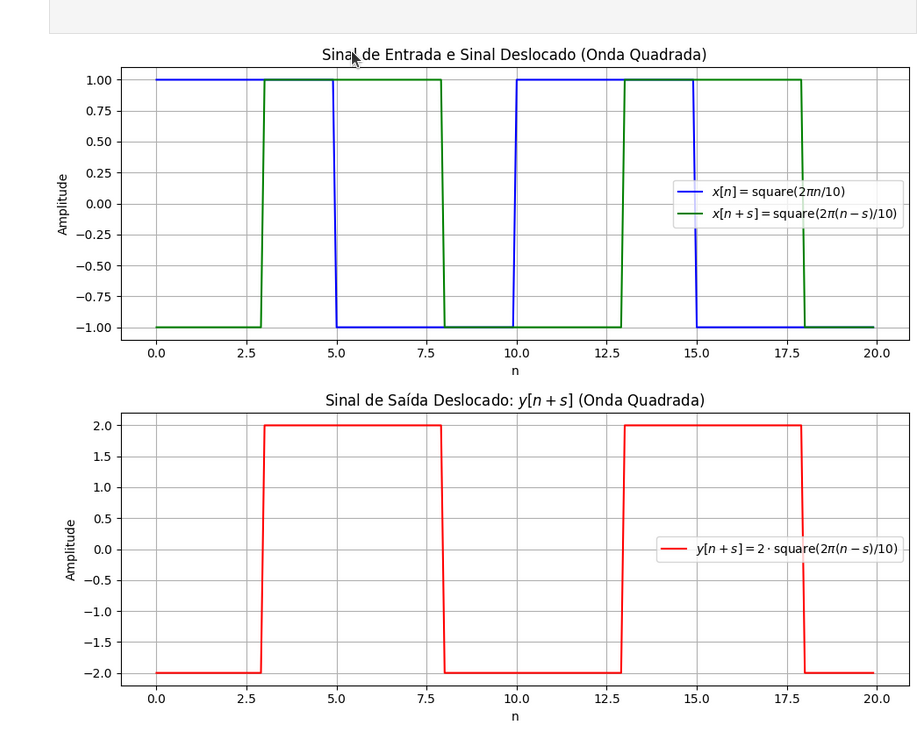
Agora usaremos o exemplo de shift, apresentando uma onda quadrada, com deslocamento.

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# Definir o intervalo de tempo discreto
n = np.arange(0, 20, 0.1)

# Definir a função de entrada x[n] como uma onda quadrada
x_n = signal.square(2 * np.pi * n / 10)

# Definir o deslocamento s
s = 3

# Aplicar o deslocamento à entrada
x_shifted = signal.square(2 * np.pi * (n - s) / 10)

# Definir a constante de escala k (sistema)
k = 2

# Aplicar o sistema ao sinal deslocado
y_shifted = k * x_shifted

# Criar os gráficos
fig, axs = plt.subplots(2, 1, figsize=(10, 8))

# Gráfico do sinal de entrada x[n] e do sinal deslocado x[n+s]
axs[0].plot(n, x_n, label='$x[n] = \mathrm{square}(2\pi n / 10)$', color='b')
axs[0].plot(n, x_shifted, label='$x[n+s] = \mathrm{square}(2\pi (n-s) / 10)$', color='g')
axs[0].set_title('Sinal de Entrada e Sinal Deslocado (Onda Quadrada)')
axs[0].set_xlabel('n')
axs[0].set_ylabel('Amplitude')
axs[0].legend()
axs[0].grid(True)

# Gráfico do sinal de saída deslocado y[n+s]
axs[1].plot(n, y_shifted, label='$y[n+s] = 2 \cdot \mathrm{square}(2\pi (n-s) / 10)$', color='r')
axs[1].set_title('Sinal de Saída Deslocado: $y[n+s]$ (Onda Quadrada)')
axs[1].set_xlabel('n')
axs[1].set_ylabel('Amplitude')
axs[1].legend()
axs[1].grid(True)

plt.tight_layout()
plt.show()

Ficando no exemplo, claramente o deslocamento.

Exercício 3

import numpy as np
import matplotlib.pyplot as plt

# Função para gerar sinais exponenciais e^(an)
def exponential(a, n):
    expo = []
    for sample in n:
        expo.append(np.exp(a * sample))
    return expo

# Definir parâmetros
a = 2
UL = 1
LL = -1
n = np.arange(LL, UL, 0.1)
x = exponential(a, n)

# Aumentar o ganho em 10x
x_gain = [10 * value for value in x]

# Somar por 5
x_add = [value + 5 for value in x]

# Subtrair por pi
x_subtract = [value - np.pi for value in x]

# Fazer um shift de 3 posições
shift = 3
n_shifted = n + shift
x_shift = exponential(a, n - shift)

# Plotar os gráficos
fig, axs = plt.subplots(4, 1, figsize=(10, 20))

# Sinal original
axs[0].stem(n, x, basefmt=" ", use_line_collection=True)
axs[0].set_xlabel('n')
axs[0].set_ylabel('x[n]')
axs[0].set_title('Exponential Signal $e^{an}$')

# Aumento de ganho em 10x
axs[1].stem(n, x_gain, basefmt=" ", use_line_collection=True)
axs[1].set_xlabel('n')
axs[1].set_ylabel('10x[n]')
axs[1].set_title('Exponential Signal $10 \cdot e^{an}$')

# Soma por 5
axs[2].stem(n, x_add, basefmt=" ", use_line_collection=True)
axs[2].set_xlabel('n')
axs[2].set_ylabel('x[n] + 5')
axs[2].set_title('Exponential Signal $e^{an} + 5$')

# Subtração por pi
axs[3].stem(n, x_subtract, basefmt=" ", use_line_collection=True)
axs[3].set_xlabel('n')
axs[3].set_ylabel('x[n] - π')
axs[3].set_title('Exponential Signal $e^{an} - π$')

# Shift de 3 posições
fig, ax = plt.subplots(figsize=(10, 5))
ax.stem(n_shifted, x_shift, basefmt=" ", use_line_collection=True)
ax.set_xlabel('n')
ax.set_ylabel('x[n-3]')
ax.set_title('Exponential Signal Shifted by 3 Positions $e^{a(n-3)}$')

plt.tight_layout()
plt.show()