Segundo trabalho de Mathlab2
3 de junho de 2023Projetos de Sistemas de Controle com o Matlab
| DISCIPLINA /AVALIAÇÃO: Tecnologia de Automação I / P1 | |||
| Grupo: 1 | |||
| Nome: Marcelo , Robson | |||
| Professor: Marcelo Duarte | |||
Primeira questão
1. (5,0 pontos) Projeto de Controladores PID.
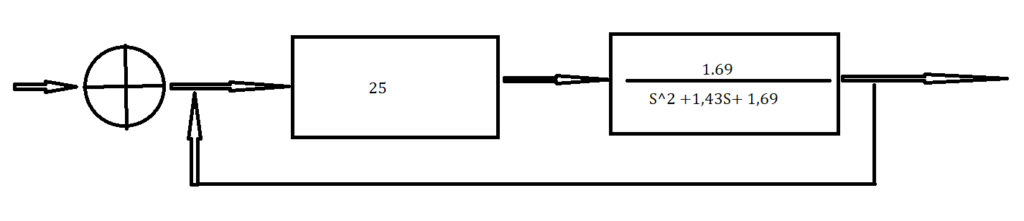
𝜁 = 0,55 𝑒 𝜔𝑛 = 1,3 𝑟𝑎𝑑/𝑠
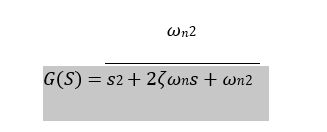
num1=[0 0 1.69];
den1=[1 1.43 1.69];
Gp1=tf(num1,den1)
Gp1=
1.69
S²+1.43s+1.69
FT1=feedback (Gp1,1)
FT1=
1.69
S²+1.43s+3.38
Step(FT1)

Para o sistema em malha fechada, integre esta planta a controladores do tipo PID de acordo com os TRÊS itens a seguir.
Item A
a) Controlador Proporcional (P)
𝐶𝑎𝑑𝑎 𝑢𝑚 𝑑𝑜𝑠 𝑔𝑟𝑢𝑝𝑜𝑠 𝑑𝑒𝑣𝑒 𝑇𝐸𝑆𝑇𝐴𝑅 𝑣𝑎𝑙𝑜𝑟𝑒𝑠 𝑑𝑒 𝐾𝑝 que “melhorem” a resposta ao degrau quando comparada à resposta do sistema sem nenhum controlador.
num2=[0 0 42.25];
den2=[1 1.43 1.69];
Gp2=tf(num2,den2)
Gp2 =
42.25
------------------
S²+ 1.43s + 1.69
Continuous-time transfer function.
FT2=feedback(Gp2,1)
FT2=
42.25
-------------------
S² + 1.43 s + 43.94
Continuous-time transfer function.
step(FT2)
O valor de 42,25, é devido a multiplicação do controle (KP) de 25, com 1,69.
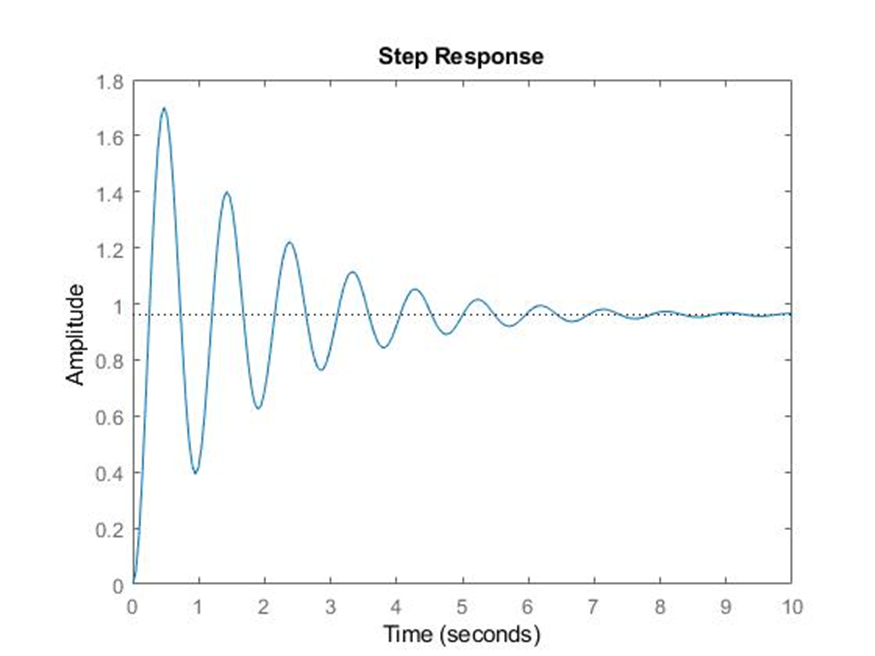
Questão B
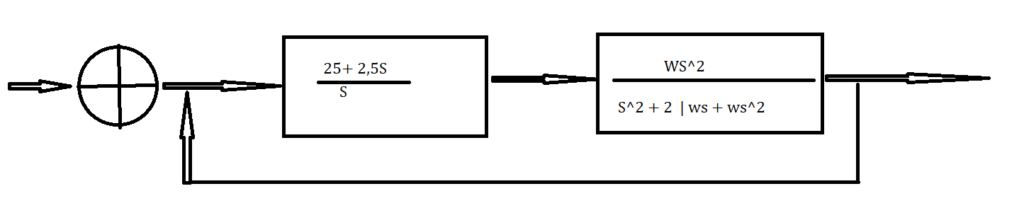
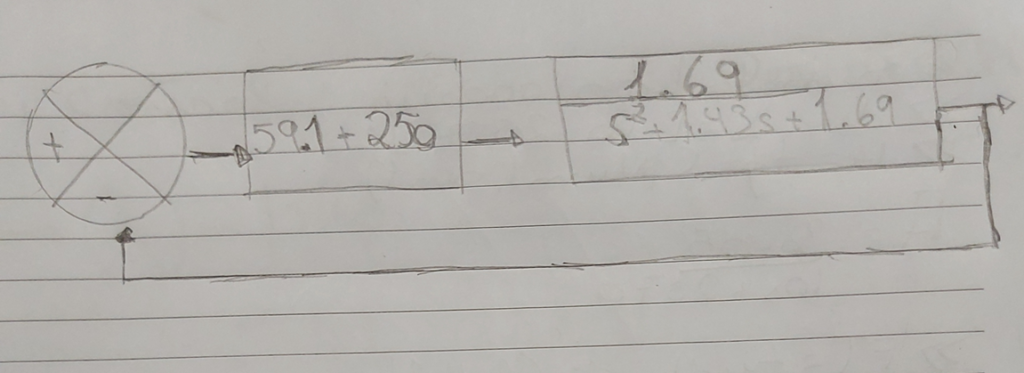
𝐶𝑎𝑑𝑎 𝑢𝑚 𝑑𝑜𝑠 𝑔𝑟𝑢𝑝𝑜𝑠 𝑑𝑒𝑣𝑒 𝑇𝐸𝑆𝑇𝐴𝑅 𝑣𝑎𝑙𝑜𝑟𝑒𝑠 𝑑𝑒 𝐾𝑝 𝑒 𝐾𝑑 que “melhorem ainda mais”
Considerando o KP
num1=[1.69];
den1=[1,1.43,1.69];
Gp1= tf(num1,den1);
num2=[59,1,250]
den2=[0,0,1]
Gp2 = tf(num2,den2)
Gp3=series(Gp1,Gp2)
ft1 = feedback(Gp3,1);
step(ft1);
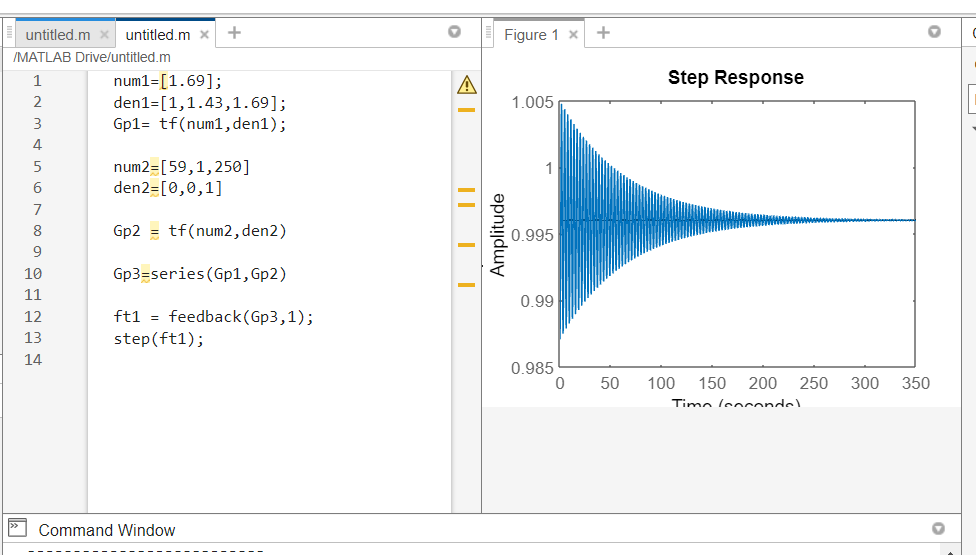
Conclusão: A amplitude ficou muito baixa, porem o tempo de resposta até estabilizar ficou extremamente longo.
Questão C
c) Controlador Proporcional Integral Derivativo (PID)
𝐶𝑎𝑑𝑎 𝑢𝑚 𝑑𝑜𝑠 𝑔𝑟𝑢𝑝𝑜𝑠 𝑑𝑒𝑣𝑒 𝑇𝐸𝑆𝑇𝐴𝑅 𝑣𝑎𝑙𝑜𝑟𝑒𝑠 𝑑𝑒 𝐾𝑝, 𝐾𝑖 𝑒 𝐾𝑑 para “melhorar DEFINITIVAMENTE” a resposta ao degrau quando comparada à resposta do sistema com o controlador proporcional-derivativo.
Atenção: você terá TRÊS (3) sistemas a modelar!
Para cada UM dos TRÊS SISTEMAS, realize as seguintes tarefas:
- (1,0 pontos) Apresente o Diagrama de Blocos para cada um dos três sistemas;
- (3,0 pontos) Apresente o gráfico da resposta ao degrau unitário para cada um dos três sistemas estabelecendo a comparação de desempenho ao se utilizar este ou aquele controlador.
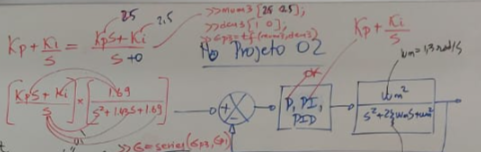
Questão A
% primeira modificação
kp=2;
ki=40;
vl=ki*1.69;
num1=[0, kp, vl ];
den1=[1, 1.43, 1.69];
Gp1=tf(num1,den1)
ft1 = feedback(Gp1,1);
step(ft1);
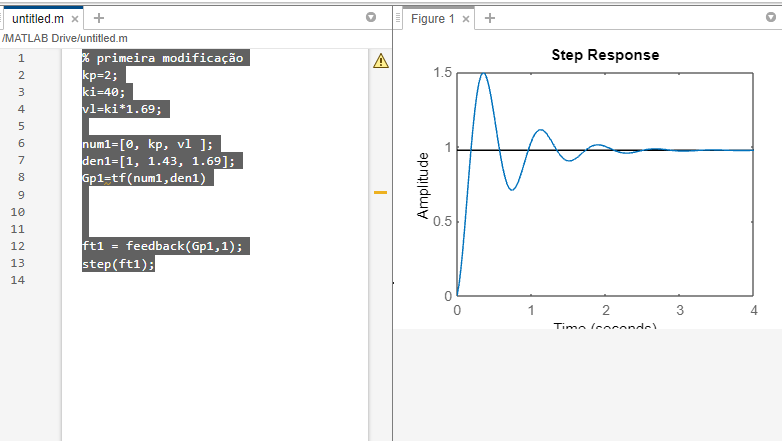
Se compararmos
Vemos que houve uma melhora da amplitude , com um tempo de resposta um pouco menor, e melhora na amplitude.
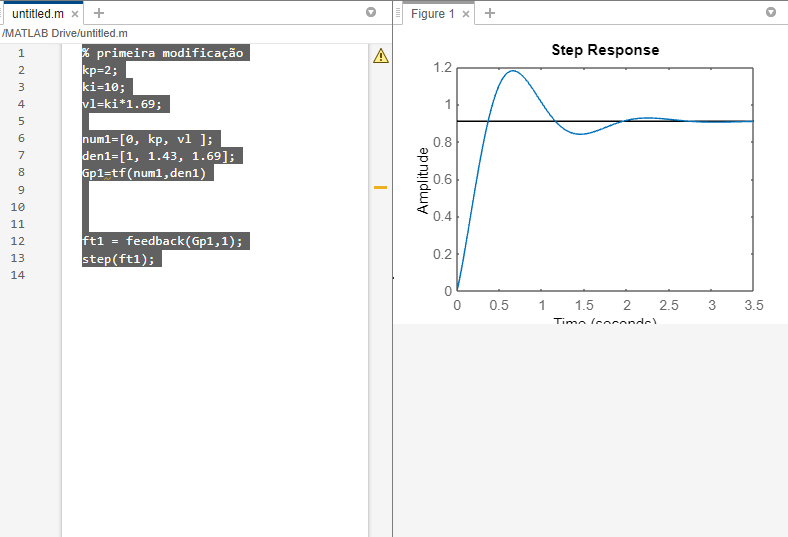
% primeira modificação
kp=2;
ki=10;
vl=ki*1.69;
num1=[0, kp, vl ];
den1=[1, 1.43, 1.69];
Gp1=tf(num1,den1)
ft1 = feedback(Gp1,1);
step(ft1);
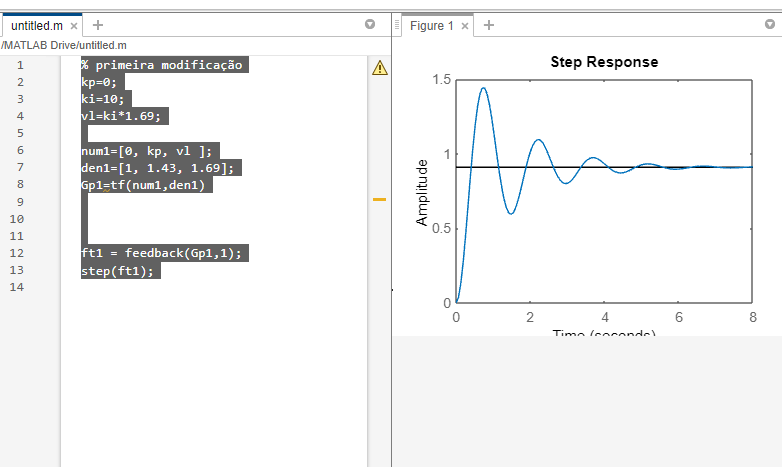
% primeira modificação
kp=0;
ki=10;
vl=ki*1.69;
num1=[0, kp, vl ];
den1=[1, 1.43, 1.69];
Gp1=tf(num1,den1)
ft1 = feedback(Gp1,1);
step(ft1);
Questão B
num1=[1.69];
den1=[1,1.43,1.69];
Gp1= tf(num1,den1);
% primeira modificação
kp=28
ki=3
num2=[kp,ki]
den2=[0,1,0]
Gp2 = tf(num2,den2)
Gp3=series(Gp1,Gp2)
ft1 = feedback(Gp3,1);
step(ft1);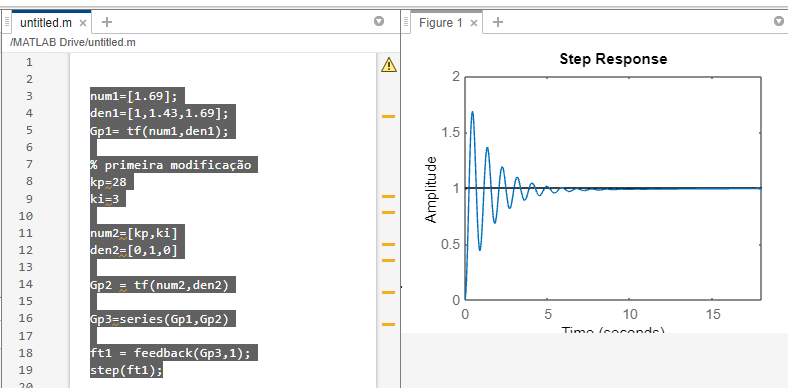
num1=[1.69];
den1=[1,1.43,1.69];
Gp1= tf(num1,den1);
% primeira modificação
kp=28
ki=0
num2=[kp,ki]
den2=[0,1,0]
Gp2 = tf(num2,den2)
Gp3=series(Gp1,Gp2)
ft1 = feedback(Gp3,1);
step(ft1);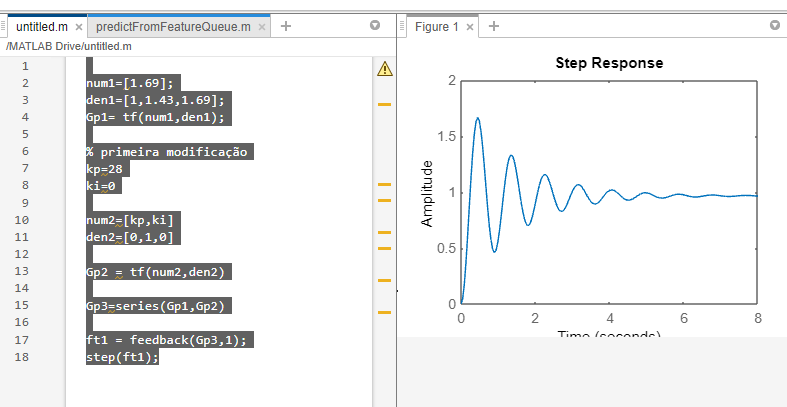
num1=[1.69];
den1=[1,1.43,1.69];
Gp1= tf(num1,den1);
% primeira modificação
kp=18
ki=2
num2=[kp,ki]
den2=[0,1,0]
Gp2 = tf(num2,den2)
Gp3=series(Gp1,Gp2)
ft1 = feedback(Gp3,1);
step(ft1);
Projeto de Controle de um Sistema Biomédico
2. (5,0 pontos) Considere um sistema simples de controle de temperatura cujo diagrama de blocos é dado a seguir;
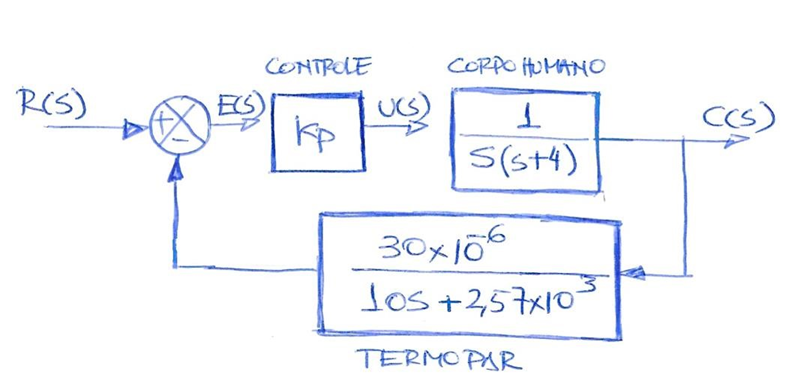
- (1,0 ponto) Encontre a função de transferência da planta sem o controlador;
num1=[ 0, 0, 1];
den1=[1, 4, 0];
G1=tf(num1,den1);
num2=[0, 0.00003];
den2=[10, 2570];
H=tf(num2,den2);
FT=feedback(G1,H,-1)
step(FT);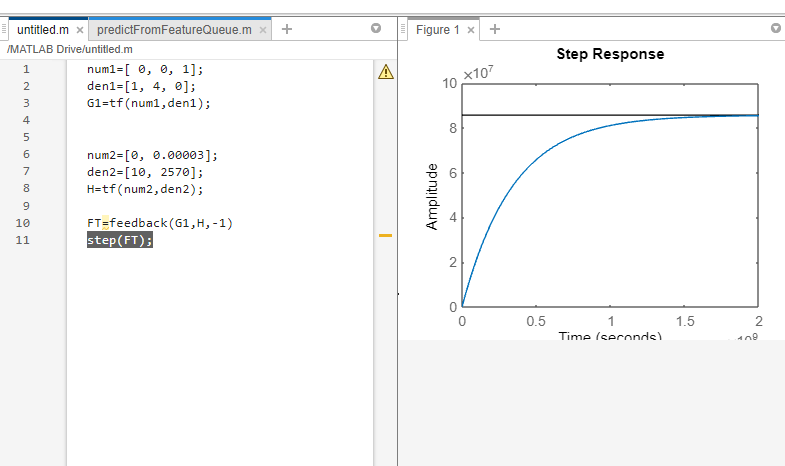
B) (3,0 pontos) Especifique ao menos dois valores para o ganho no intervalo dado por
20 < 𝐾𝑝 < 40 e 90 < 𝐾𝑝 < 120 .Encontre graficamente as respostas à rampa para os dois sistemas gerados;
Kp= 25
num1=[ 0, 0, 25];
den1=[1, 4, 0];
G1=tf(num1,den1);
num2=[0, 0.00003];
den2=[10, 2570];
H=tf(num2,den2);
FT=feedback(G1,H,-1)
step(FT)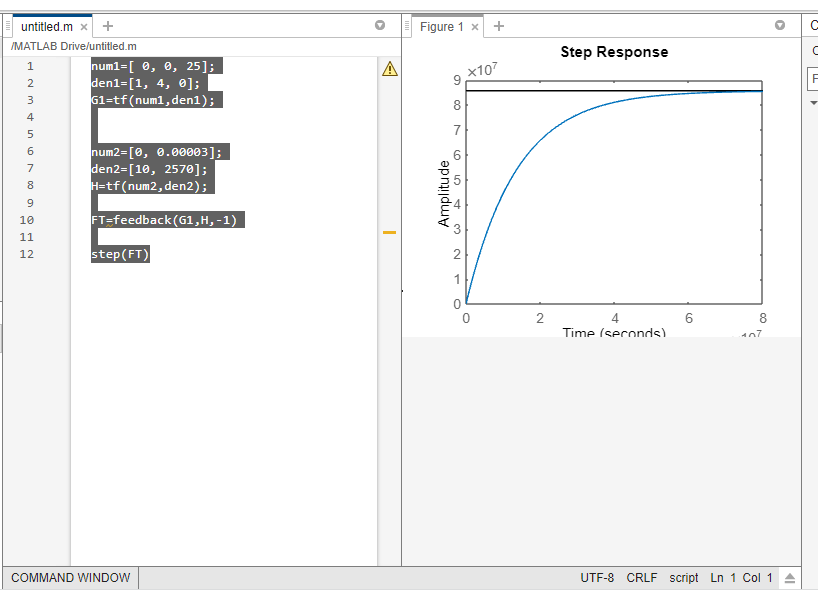
AGORA PEGANDO kp= 110
num1=[ 0, 0, 110];
den1=[1, 4, 0];
G1=tf(num1,den1);
num2=[0, 0.00003];
den2=[10, 2570];
H=tf(num2,den2);
FT=feedback(G1,H,-1)
step(FT)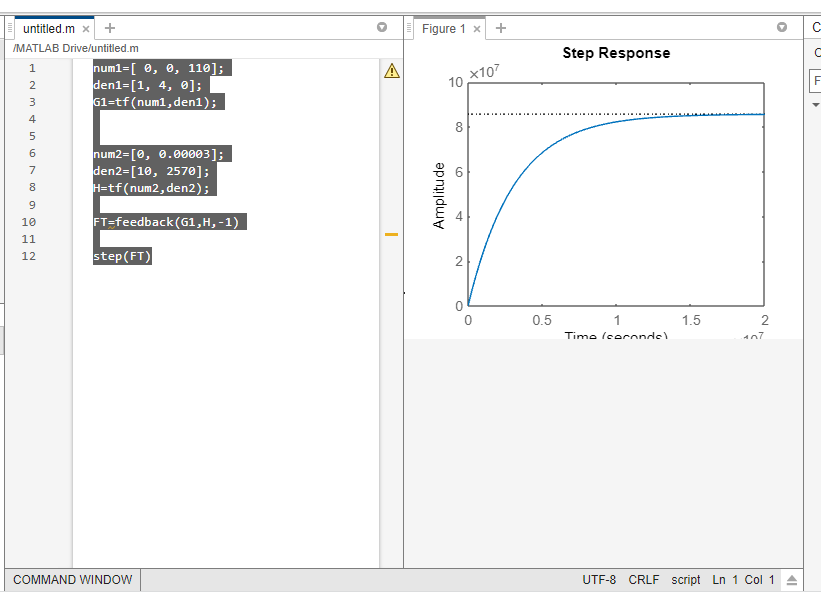
Questão C
(1,0 pontos) Compare as curvas encontradas para os dois valores distintos de 𝐾𝑝 referentes à resposta do sistema à rampa unitária.
Kp=25
O gráfico da direita é o representado por KP=110, enquanto o grafico da esquerda o kp=25.
Podemos ver uma diferença grande no tempo de resposta, enquanto o de 25, demora 8 segundos para obter amplitude, o de 110, consegue resultados muito próximos em apenas 2, tendo uma melhora considerável do tempo.
Outro ponto importante é que a curva do kp de 110, é mais suave que a dede 25, apresendo um “cotovelo” menos promeniente.
