Trabalhando com Matriz de Confusão
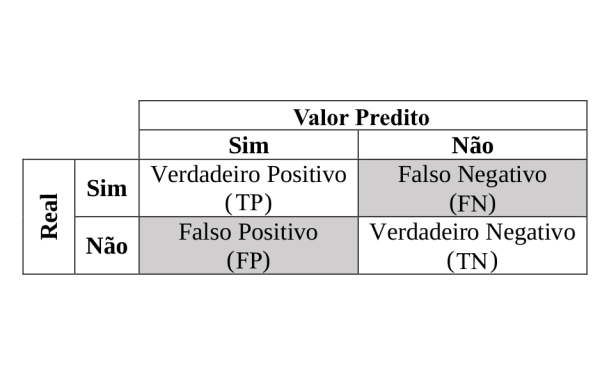
Acurácia
Diz os acertos:
Soma-se os Verdadeiros Positivos + Verdadeiros Negativos dividido pelo total de itens
onde:
a = acuracia
VP = Verdadeiro Positivo
VN = Verdadeiro Negativo
T = Total de itens
Erros
Calcula o percentual de erros na matriz de confusão
Onde:
e = Percentual de erro
FP = Falso Positivo
FN = Falso Negativo
T = Total
Sensibilidade (Sensivity) ou Repescagem (RECALL)
Onde é possível medir a sensibilidade ao acerto.
onde:
pv = Positivo Verdadeiro
VP = Verdadeiro Positivo
FN = Falso Negativo
Precisão ou Precision
Diz quanto da amostra os acertos realmente são eficientes
Onde:
p = Precisão
VP = Verdadeiro Positivo
FP = Falso Positivo
Negativo Verdadeiros ou Especificidade (Specifity)
Diz dos Negativos, quantos foram corretamente classificados.
Onde:
nv = Especificidade
VN = Verdadeiro Negativo
FP = Falso Positivo
Erro do Tipo 1 ou Positivo Falso
Onde de todos os Negativos, quantos foram classificados incorretamente
Onde:
pf = Positivo Falso
FP = Falso Positivo
VN = Verdadeiro Negativo
FP = Falso Positivo
Negativos Falsos ou Erro do Tipo II
De todos os Positivos, quantos foram classificados incorretamente como Negativo
Onde:
nf = Negativos Falsos
FN = Falso Negativos
VP = Verdadeiros Positivos
FN = Falso Negativos
F1 Score
Maximiza os acertos, com relação a precisão, onde valores mais próximos ao 1 são desejados.
Onde:
F1 = Score
p = Precisão ou Precision
r = Sensibilidade (Sensivity) ou Repescagem (RECALL)
Logarithmic Loss (Perda Logarítmica)
A perda logarítmica, também conhecida como log loss ou cross-entropy loss, é uma medida de desempenho usada em problemas de classificação, especialmente em classificações binárias e multiclasse. Essa métrica quantifica quão distantes estão as probabilidades previstas de um modelo em relação aos valores verdadeiros ou reais (0 ou 1). A ideia é penalizar não apenas as classificações incorretas, mas também a confiança errada nas previsões.
Para uma previsão perfeita, a perda logarítmica é 0, e ela aumenta à medida que a previsão se afasta do valor real. Um aspecto importante da perda logarítmica é que ela penaliza severamente as previsões que estão confiantemente erradas. Por exemplo, uma previsão errada com alta certeza (por exemplo, prever a probabilidade de uma classe como 0.9 quando a classe verdadeira é a outra) resultará em uma penalidade maior do que uma previsão errada com baixa certeza.
A fórmula para a perda logarítmica em classificação binária é dada por:
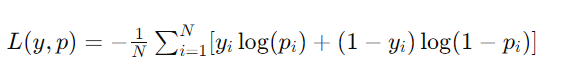
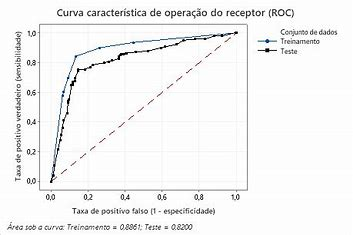
Receiver Operator Characteristic (ROC)
A Característica de Operação do Receptor (ROC, do inglês “Receiver Operating Characteristic”) é uma ferramenta utilizada para avaliar o desempenho de modelos de classificação binária. Ela é representada graficamente por uma curva que compara a taxa de verdadeiros positivos (sensibilidade) com a taxa de falsos positivos (1 – especificidade), para diferentes limiares de decisão.
A área sob a curva ROC (AUC, do inglês “Area Under the ROC Curve”) é um indicador da capacidade do modelo de discriminar entre as duas classes. Um valor de AUC igual a 1 indica um modelo perfeito, capaz de separar completamente as duas classes sem erros. Um valor de AUC igual a 0,5 sugere um desempenho não melhor do que o acaso, ou seja, o modelo não tem capacidade de discriminação entre as classes.
A curva ROC é particularmente útil porque permite a avaliação do desempenho do modelo em diferentes limiares, facilitando a escolha de um ponto de corte que equilibre entre a captura de verdadeiros positivos e a minimização de falsos positivos, de acordo com o contexto e os custos associados a cada tipo de erro.
AUC – Area Under Curve
AUC, que significa “Área Sob a Curva”, é um termo amplamente utilizado em análise de dados e machine learning, especialmente quando se refere à Curva ROC (Característica de Operação do Receptor). A AUC é uma métrica que quantifica o desempenho geral de um modelo de classificação, independentemente do limiar de decisão aplicado.
Características Principais da AUC
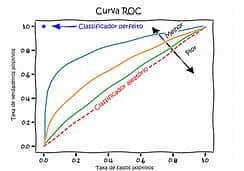
- Avaliação de Desempenho: A AUC mede a capacidade do modelo de discriminar entre classes positivas e negativas. Um modelo com uma AUC de 1.0 é considerado perfeito, capaz de separar perfeitamente as duas classes. Um modelo com uma AUC de 0.5 não tem capacidade de discriminação, equivalente a um palpite aleatório.
- Independente do Limiar: A AUC é particularmente útil porque é independente do ponto de corte escolhido. Isso significa que ela fornece uma medida do desempenho do modelo que não é afetada pela seleção de um limiar específico para a classificação de positivos e negativos.
- Comparação de Modelos: A AUC permite comparar o desempenho de diferentes modelos de classificação diretamente. Um modelo com uma AUC maior é geralmente considerado melhor na discriminação das classes.
- Aplicável em Diversos Contextos: Embora frequentemente associada à Curva ROC, o conceito de AUC pode ser aplicado a outras curvas, como a Curva Precision-Recall, especialmente em contextos onde as classes são muito desbalanceadas.
Limitações
- Não Capta Todas as Dimensões de Desempenho: Embora a AUC forneça uma medida útil do desempenho geral de um modelo, ela não captura todas as nuances, como o equilíbrio entre sensibilidade e especificidade ou a precisão das previsões positivas (precisão).
- Desbalanceamento de Classes: Em situações com desbalanceamento acentuado de classes, a AUC pode ser enganosa, sugerindo um desempenho melhor do que o modelo realmente apresenta, especialmente se a preocupação é com a precisão da classificação da classe minoritária.
Conclusão
A AUC é uma métrica valiosa para avaliar e comparar modelos de classificação, oferecendo uma visão geral da capacidade do modelo de discriminar entre classes. Contudo, é importante considerá-la junto a outras métricas para obter uma avaliação completa do desempenho do modelo.

