Controladores PID – Definições
SP – Set Point – Variaveis que se deseja controlar.
PV- Variável de processo – Indica o sensores, que dão as entradas ou medições iniciais.
SP- Variável desejada – Indica o valor que se deseja obter “desejado”
SP – Set Point – Variaveis que se deseja controlar.
PV- Variável de processo – Indica o sensores, que dão as entradas ou medições iniciais.
SP- Variável desejada – Indica o valor que se deseja obter “desejado”
| DISCIPLINA /AVALIAÇÃO: Tecnologia de Automação I / P1 | |||
| Grupo: 1 | |||
| Nome: Marcelo , Robson | |||
| Professor: Marcelo Duarte | |||
1. (5,0 pontos) Projeto de Controladores PID.
𝜁 = 0,55 𝑒 𝜔𝑛 = 1,3 𝑟𝑎𝑑/𝑠
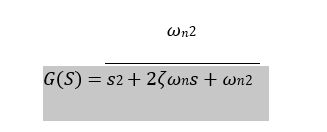
num1=[0 0 1.69];
den1=[1 1.43 1.69];
Gp1=tf(num1,den1)
Gp1=
1.69
S²+1.43s+1.69
FT1=feedback (Gp1,1)
FT1=
1.69
S²+1.43s+3.38
Step(FT1)

Para o sistema em malha fechada, integre esta planta a controladores do tipo PID de acordo com os TRÊS itens a seguir.
𝐶𝑎𝑑𝑎 𝑢𝑚 𝑑𝑜𝑠 𝑔𝑟𝑢𝑝𝑜𝑠 𝑑𝑒𝑣𝑒 𝑇𝐸𝑆𝑇𝐴𝑅 𝑣𝑎𝑙𝑜𝑟𝑒𝑠 𝑑𝑒 𝐾𝑝 que “melhorem” a resposta ao degrau quando comparada à resposta do sistema sem nenhum controlador.
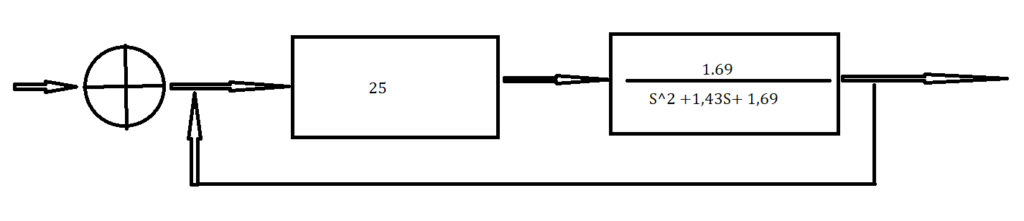
num2=[0 0 42.25];
den2=[1 1.43 1.69];
Gp2=tf(num2,den2)
Gp2 =
42.25
------------------
S²+ 1.43s + 1.69
Continuous-time transfer function.
FT2=feedback(Gp2,1)
FT2=
42.25
-------------------
S² + 1.43 s + 43.94
Continuous-time transfer function.
step(FT2)
O valor de 42,25, é devido a multiplicação do controle (KP) de 25, com 1,69.
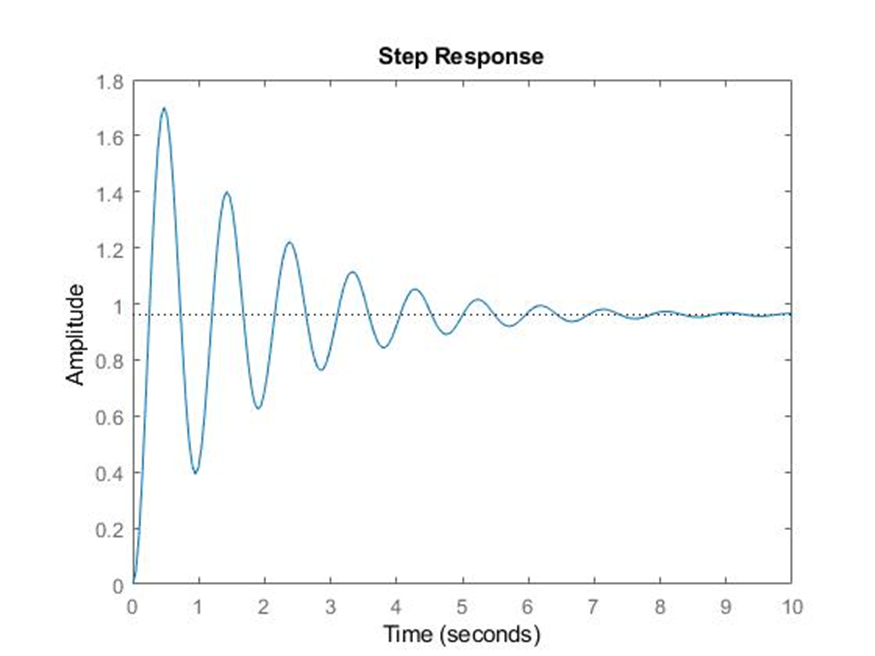
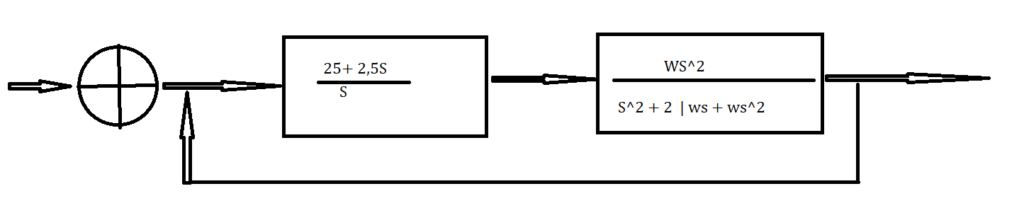
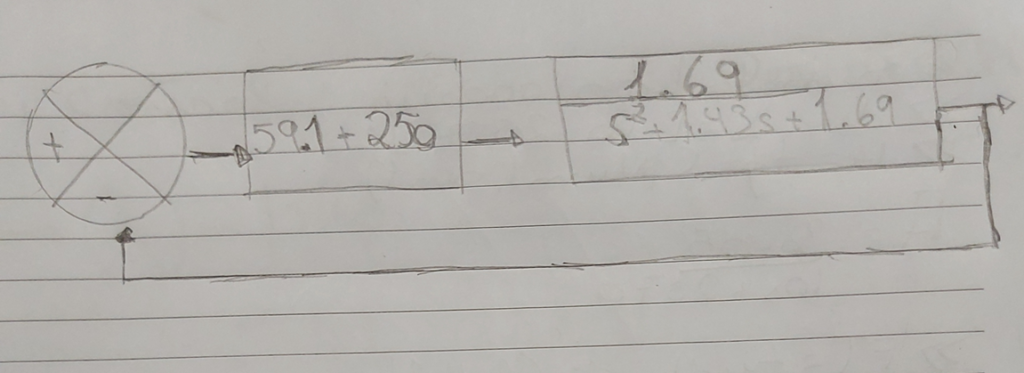
𝐶𝑎𝑑𝑎 𝑢𝑚 𝑑𝑜𝑠 𝑔𝑟𝑢𝑝𝑜𝑠 𝑑𝑒𝑣𝑒 𝑇𝐸𝑆𝑇𝐴𝑅 𝑣𝑎𝑙𝑜𝑟𝑒𝑠 𝑑𝑒 𝐾𝑝 𝑒 𝐾𝑑 que “melhorem ainda mais”
Considerando o KP
num1=[1.69];
den1=[1,1.43,1.69];
Gp1= tf(num1,den1);
num2=[59,1,250]
den2=[0,0,1]
Gp2 = tf(num2,den2)
Gp3=series(Gp1,Gp2)
ft1 = feedback(Gp3,1);
step(ft1);
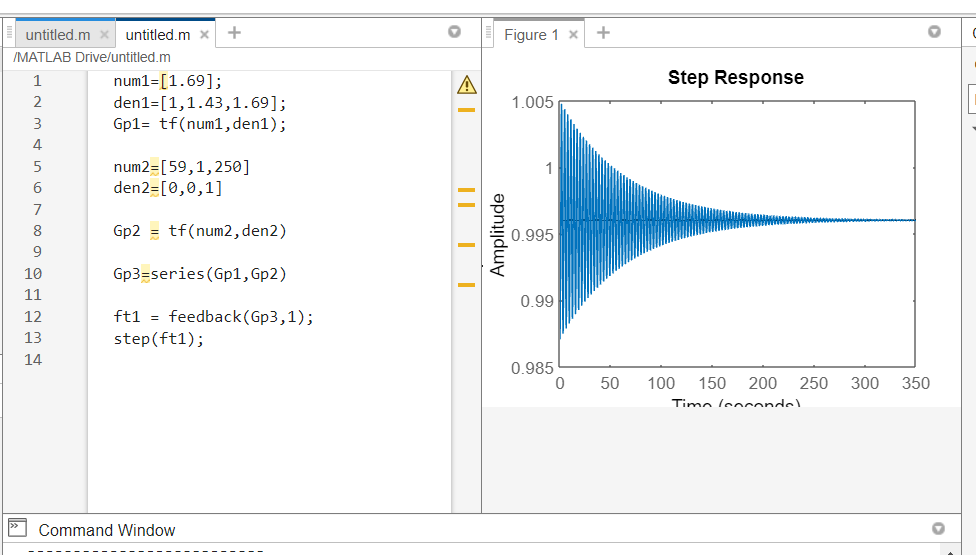
Conclusão: A amplitude ficou muito baixa, porem o tempo de resposta até estabilizar ficou extremamente longo.
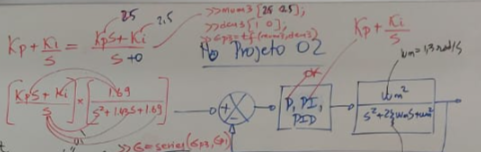
𝐶𝑎𝑑𝑎 𝑢𝑚 𝑑𝑜𝑠 𝑔𝑟𝑢𝑝𝑜𝑠 𝑑𝑒𝑣𝑒 𝑇𝐸𝑆𝑇𝐴𝑅 𝑣𝑎𝑙𝑜𝑟𝑒𝑠 𝑑𝑒 𝐾𝑝, 𝐾𝑖 𝑒 𝐾𝑑 para “melhorar DEFINITIVAMENTE” a resposta ao degrau quando comparada à resposta do sistema com o controlador proporcional-derivativo.
Atenção: você terá TRÊS (3) sistemas a modelar!
Para cada UM dos TRÊS SISTEMAS, realize as seguintes tarefas:
Questão A
% primeira modificação
kp=2;
ki=40;
vl=ki*1.69;
num1=[0, kp, vl ];
den1=[1, 1.43, 1.69];
Gp1=tf(num1,den1)
ft1 = feedback(Gp1,1);
step(ft1);
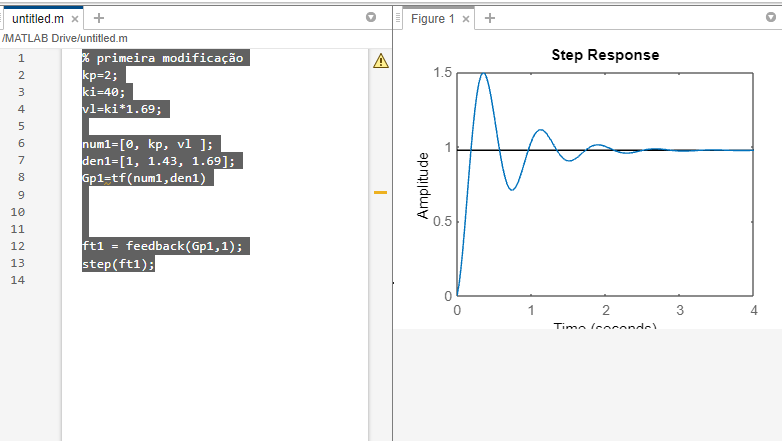
Se compararmos
Vemos que houve uma melhora da amplitude , com um tempo de resposta um pouco menor, e melhora na amplitude.
% primeira modificação
kp=2;
ki=10;
vl=ki*1.69;
num1=[0, kp, vl ];
den1=[1, 1.43, 1.69];
Gp1=tf(num1,den1)
ft1 = feedback(Gp1,1);
step(ft1);
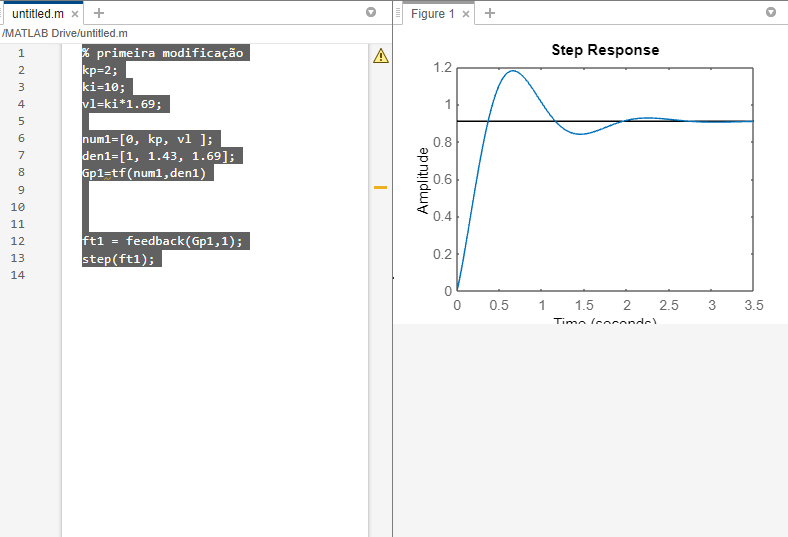
% primeira modificação
kp=0;
ki=10;
vl=ki*1.69;
num1=[0, kp, vl ];
den1=[1, 1.43, 1.69];
Gp1=tf(num1,den1)
ft1 = feedback(Gp1,1);
step(ft1);
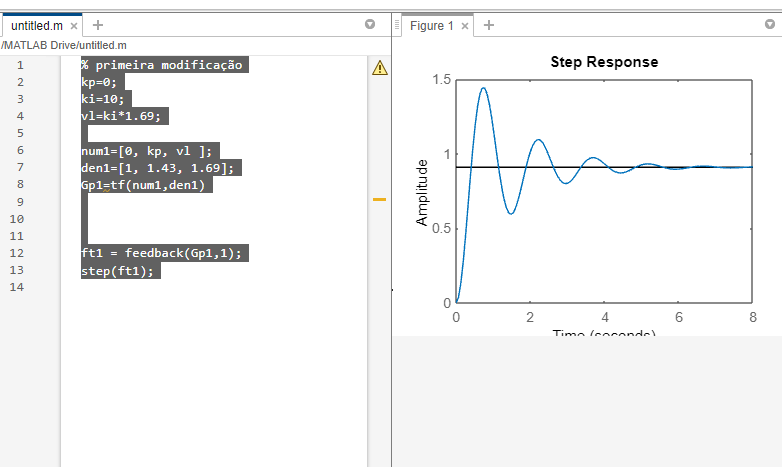
Questão B
num1=[1.69];
den1=[1,1.43,1.69];
Gp1= tf(num1,den1);
% primeira modificação
kp=28
ki=3
num2=[kp,ki]
den2=[0,1,0]
Gp2 = tf(num2,den2)
Gp3=series(Gp1,Gp2)
ft1 = feedback(Gp3,1);
step(ft1);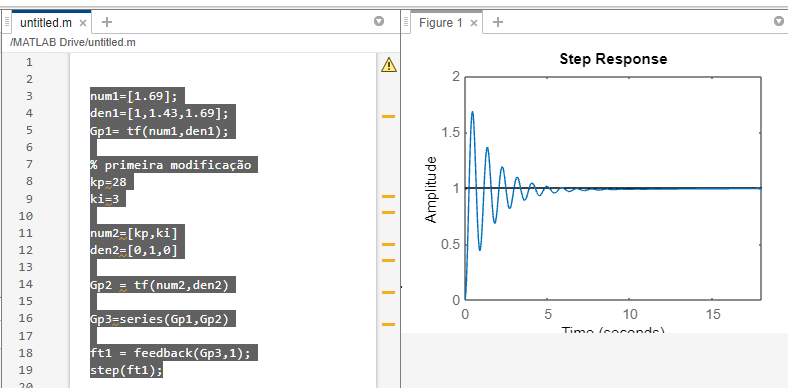
num1=[1.69];
den1=[1,1.43,1.69];
Gp1= tf(num1,den1);
% primeira modificação
kp=28
ki=0
num2=[kp,ki]
den2=[0,1,0]
Gp2 = tf(num2,den2)
Gp3=series(Gp1,Gp2)
ft1 = feedback(Gp3,1);
step(ft1);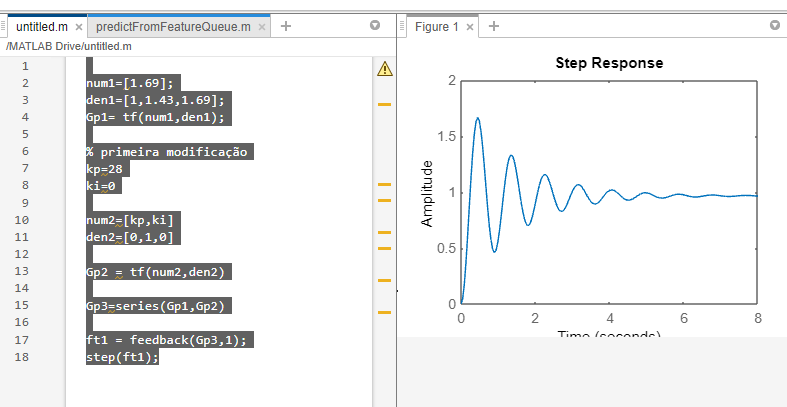
num1=[1.69];
den1=[1,1.43,1.69];
Gp1= tf(num1,den1);
% primeira modificação
kp=18
ki=2
num2=[kp,ki]
den2=[0,1,0]
Gp2 = tf(num2,den2)
Gp3=series(Gp1,Gp2)
ft1 = feedback(Gp3,1);
step(ft1);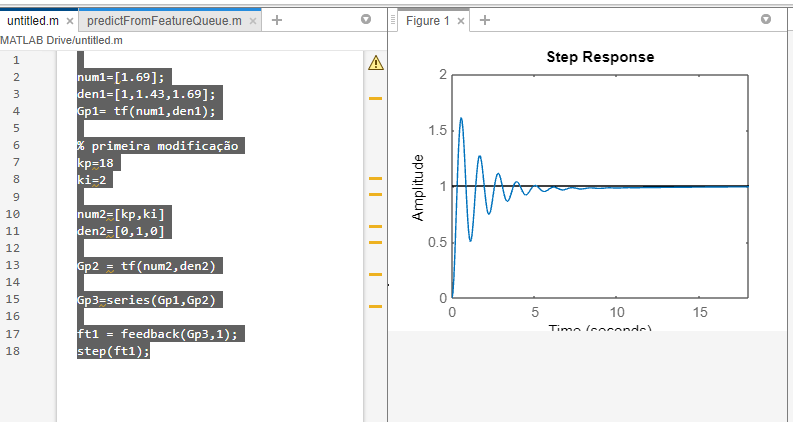
2. (5,0 pontos) Considere um sistema simples de controle de temperatura cujo diagrama de blocos é dado a seguir;
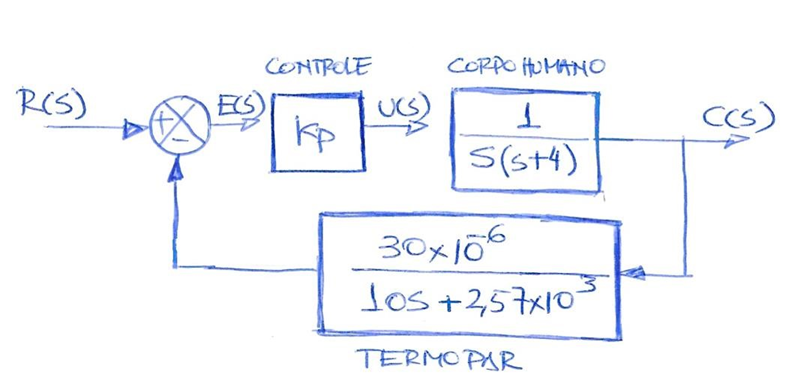
num1=[ 0, 0, 1];
den1=[1, 4, 0];
G1=tf(num1,den1);
num2=[0, 0.00003];
den2=[10, 2570];
H=tf(num2,den2);
FT=feedback(G1,H,-1)
step(FT);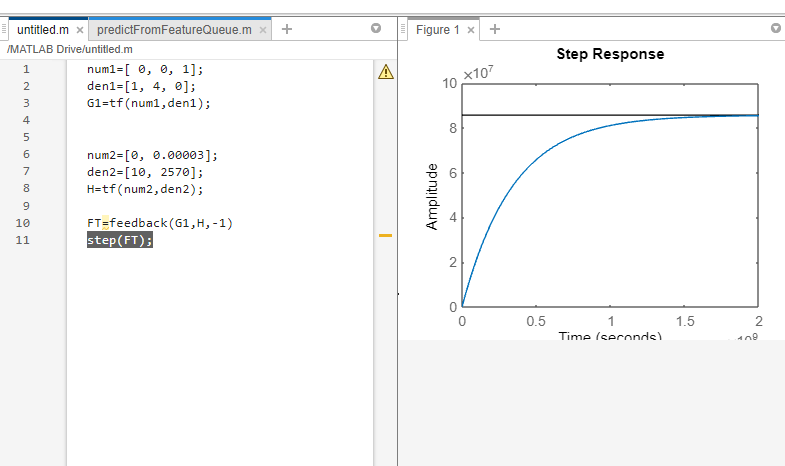
B) (3,0 pontos) Especifique ao menos dois valores para o ganho no intervalo dado por
20 < 𝐾𝑝 < 40 e 90 < 𝐾𝑝 < 120 .Encontre graficamente as respostas à rampa para os dois sistemas gerados;
Kp= 25
num1=[ 0, 0, 25];
den1=[1, 4, 0];
G1=tf(num1,den1);
num2=[0, 0.00003];
den2=[10, 2570];
H=tf(num2,den2);
FT=feedback(G1,H,-1)
step(FT)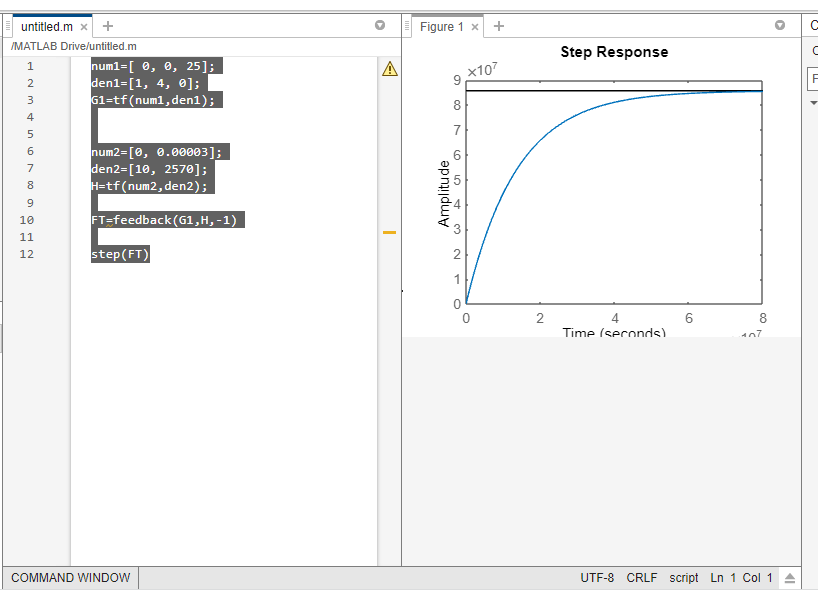
AGORA PEGANDO kp= 110
num1=[ 0, 0, 110];
den1=[1, 4, 0];
G1=tf(num1,den1);
num2=[0, 0.00003];
den2=[10, 2570];
H=tf(num2,den2);
FT=feedback(G1,H,-1)
step(FT)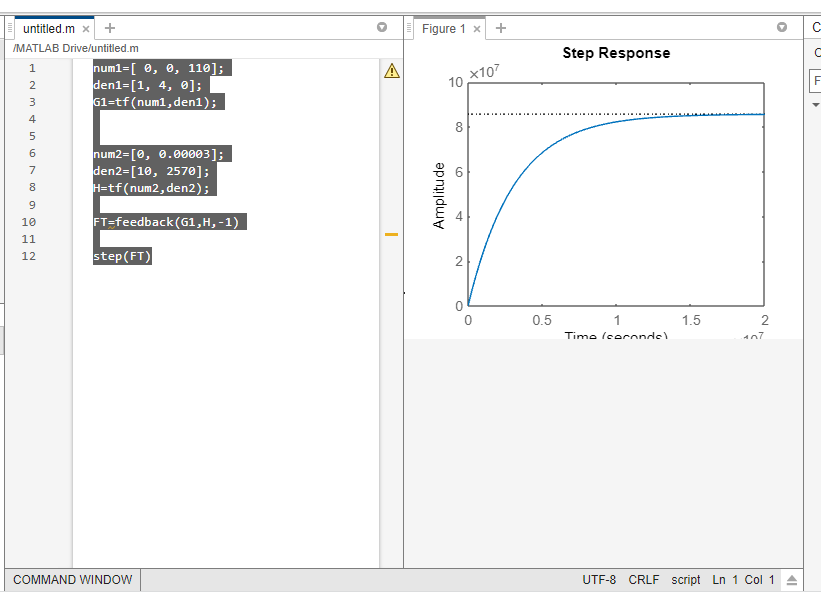
(1,0 pontos) Compare as curvas encontradas para os dois valores distintos de 𝐾𝑝 referentes à resposta do sistema à rampa unitária.
Kp=25
O gráfico da direita é o representado por KP=110, enquanto o grafico da esquerda o kp=25.
Podemos ver uma diferença grande no tempo de resposta, enquanto o de 25, demora 8 segundos para obter amplitude, o de 110, consegue resultados muito próximos em apenas 2, tendo uma melhora considerável do tempo.
Outro ponto importante é que a curva do kp de 110, é mais suave que a dede 25, apresendo um “cotovelo” menos promeniente.
O Octave é uma linguagem de programação de alto nível e um ambiente de desenvolvimento numérico, projetado para realizar cálculos numéricos e análises científicas. Ele fornece uma interface fácil de usar para a manipulação de matrizes, implementação de algoritmos, criação de gráficos e solução de problemas numéricos em geral.
Características do Octave:
Em resumo, o Octave é uma ferramenta poderosa para realizar cálculos numéricos, análises científicas e implementação de algoritmos, sendo uma alternativa popular ao MATLAB.
Ele é amplamente utilizado por pesquisadores, engenheiros, cientistas e estudantes em diversas áreas acadêmicas e industriais.
O Octave pode ser baixado através do seguinte site:
Baixe o arquivo octave para a plataforma alvo, conforme figura abaixo:
Octave código
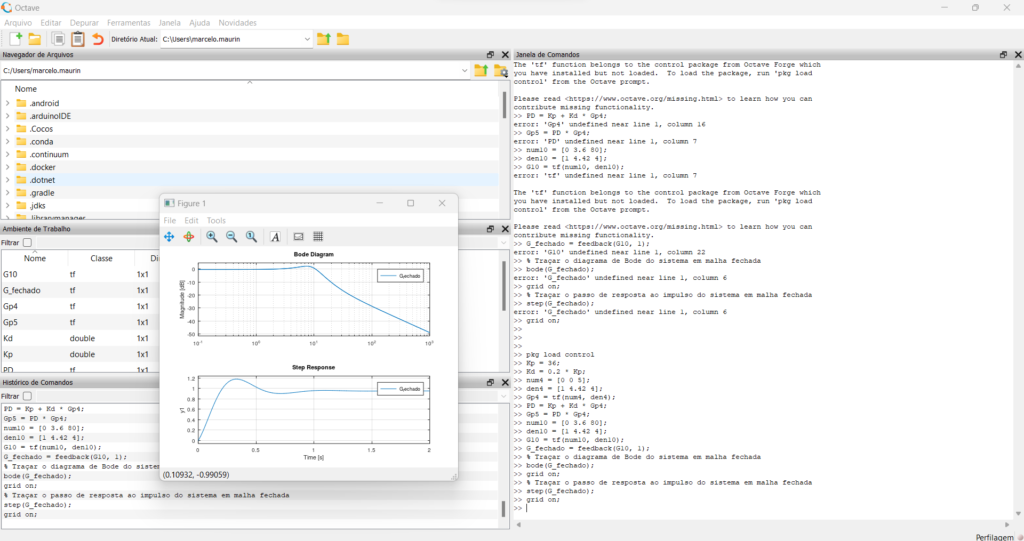
Fonte do projeto:
pkg load control
Kp = 36;
Kd = 0.2 * Kp;
num4 = [0 0 5];
den4 = [1 4.42 4];
Gp4 = tf(num4, den4);
PD = Kp + Kd * Gp4;
Gp5 = PD * Gp4;
num10 = [0 3.6 80];
den10 = [1 4.42 4];
G10 = tf(num10, den10);
G_fechado = feedback(G10, 1);
% Traçar o diagrama de Bode do sistema em malha fechada
bode(G_fechado);
grid on;
% Traçar o passo de resposta ao impulso do sistema em malha fechada
step(G_fechado);
grid on;
Neste fragmento, podemos notar as semelhanças entre os códigos:
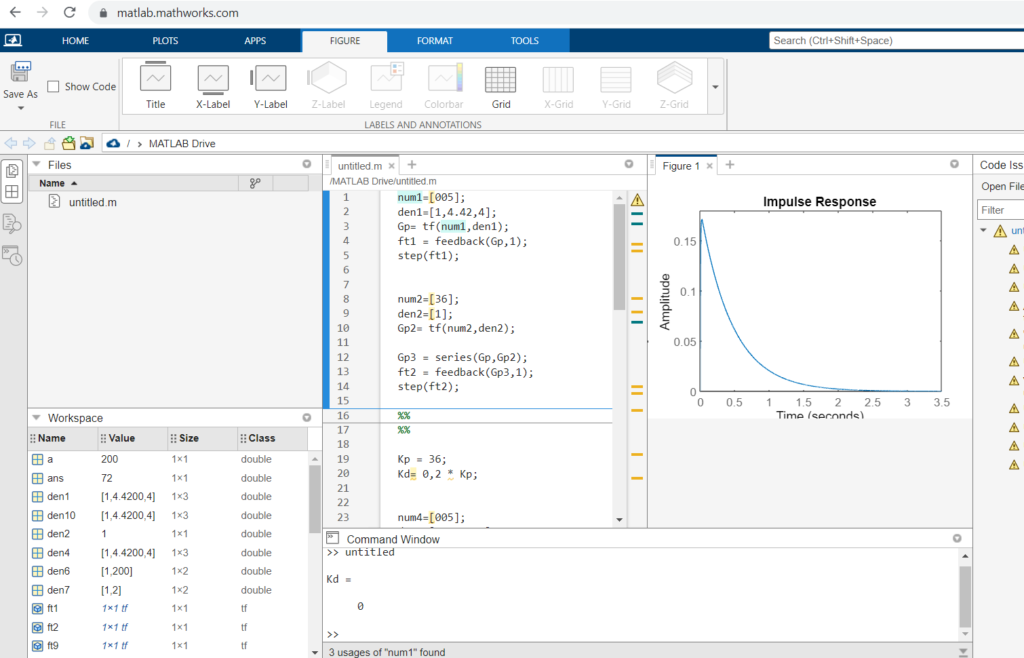
Agora iremos ver o código do projeto.
num1=[005];
den1=[1,4.42,4];
Gp= tf(num1,den1);
ft1 = feedback(Gp,1);
step(ft1);
num2=[36];
den2=[1];
Gp2= tf(num2,den2);
Gp3 = series(Gp,Gp2);
ft2 = feedback(Gp3,1);
step(ft2);
%%
%%
Kp = 36;
Kd= 0,2 * Kp;
num4=[005];
den4=[1,4.42,4];
Gp4= tf(num4,den4);
%PD = Kp+ Kd * Gp4b ;
%Gp5 = PD * Gp4;
num10=[0,3.6,80];
den10=[1,4.42,4];
G10= tf(num10,den10);
G_fechado= feedback(G10,1);
% G_fechado = feedback(Gp5,1);
step(G_fechado)
%%
s=tf('s');
num6=[1];
den6=[1,2];
uGp6=tf(num6,den6);
num7=[1];
den7=[1,2];
mGp7=tf(num7,den7);
G8=series(uGp6,mGp7);
ft9=feedback(G8,1);
impulse(ft9);
%%
%%
s=tf('s');
num6=[1];
a=200;
den6=[1,a];
uGp6=tf(num6,den6);
num7=[1];
den7=[1,2];
mGp7=tf(num7,den7);
G8=series(uGp6,mGp7);
G9= Kp*G8;
ft9=feedback(G9,1);
impulse(ft9);

| DISCIPLINA /AVALIAÇÃO: Tecnologia de Automação I / P1 | |||
| Grupo: 1 | |||
| Nome: Marcelo , Robson | |||
| Professor: Marcelo Duarte | |||
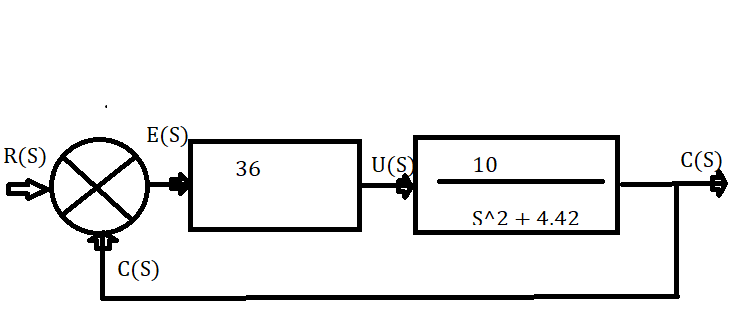
Considere um sistema de controle em malha fechada com realimentação unitária em que a planta é de segunda ordem com a seguinte função de transferência
𝐺𝑝(𝑆) =
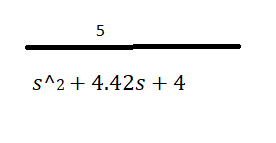
(1,0 ponto) Encontre a função de transferência em malha fechada e verifique graficamente a resposta ao degrau com o MATLAB.
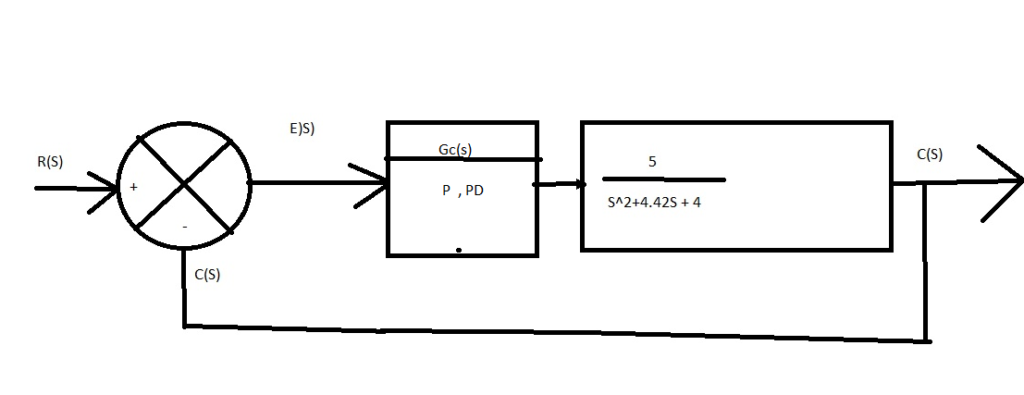
Integre a esta planta do sistema em malha fechada a controladores do tipo PID de acordo com as DUAS alternativas a seguir.
𝐺𝑟𝑢𝑝𝑜 01
𝐾𝑝 = 36
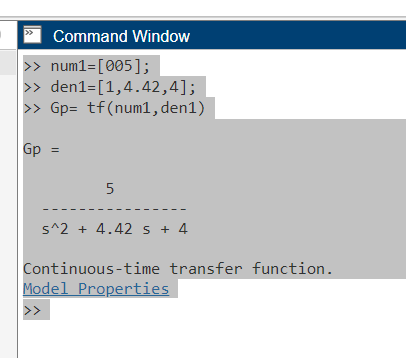
Onde fica num1 o 5
a função ficaria 1, do S^2-> 1S^2 -> 1;
o 4.42 S -> ficaria como segundo nro.
e o ultimo o nro 4.
Ficando [1,4.42,4]
>> num1=[005];
>> den1=[1,4.42,4];
>> Gp= tf(num1,den1)
Gp =
5
----------------
s^2 + 4.42 s + 4
Continuous-time transfer function.Model Properties
>> Agora vamos montar o grafico.
ft1 = feedback(Gp,1);
step(ft1);
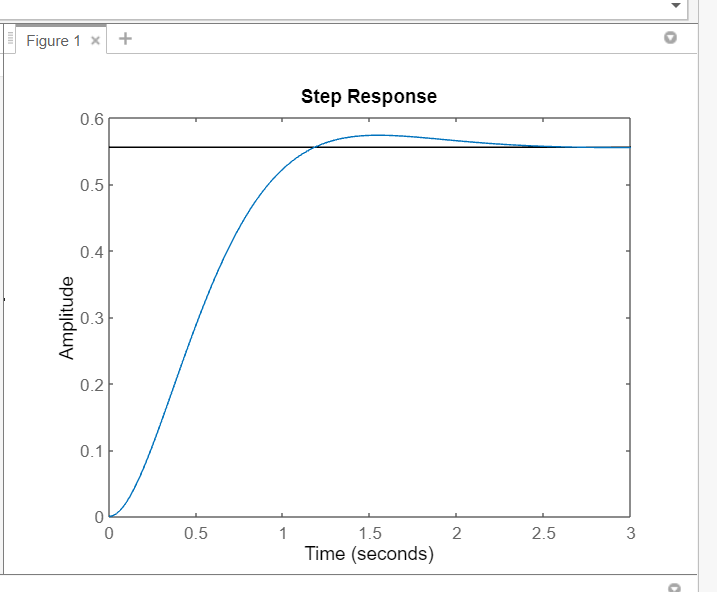
a) Controlador Proporcional (P)
𝐺𝑟𝑢𝑝𝑜 01
𝐾𝑝 = 36
|Gc(s) = Kp
Gc(s) = Kp+kdS
TEMOS A função:
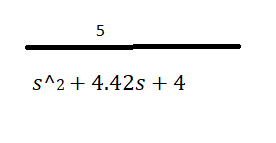
Criamos a segunda função, pela multiplicação do Gc * Gp:
Onde obtemos a função G10:
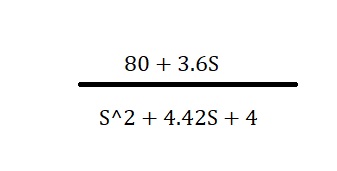
Kp = 36;
Kd= 0,2 * Kp;
num4=[005];
den4=[1,4.42,4];
Gp4= tf(num1,den1);
%PD = Kp+ Kd * Gp4b ;
%Gp5 = PD * Gp4;
num10=[0,3.6,80];
den10=[1,4.42,4];
G10= tf(num10,den10);
G_fechado= feedback(G10,1);
De posse destas informações
Geramos o gráfico abaixo:
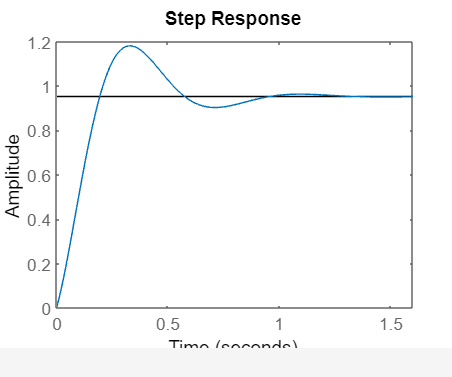
Conforme apresentado em:
http://www.ece.ufrgs.br/~jmgomes/pid/Apostila/apostila/node29.html
O Controlador Proporcional-Derivativo (PD)
A ação derivativa quando combinada com a ação proporcional tem justamente a função de “antecipar” a ação de controle a fim de que o processo reaja mais rápido. Neste caso, o sinal de controle a ser aplicado é proporcional a uma predição da saída do processo.
𝐺𝑟𝑢𝑝𝑜 01
𝐾𝑝 = 36
𝐾𝑑 = 2% 𝑑𝑒 𝐾p
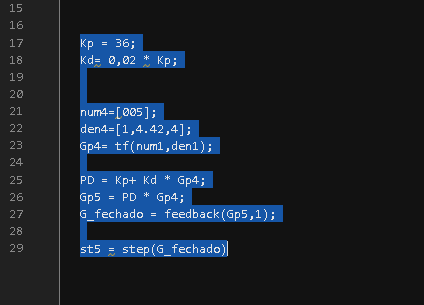
Kp = 36;
Kd= 0,02 * Kp;
num4=[005];
den4=[1,4.42,4];
Gp4= tf(num1,den1);
PD = Kp+ Kd * Gp4;
Gp5 = PD * Gp4;
G_fechado = feedback(Gp5,1);
st5 = step(G_fechado)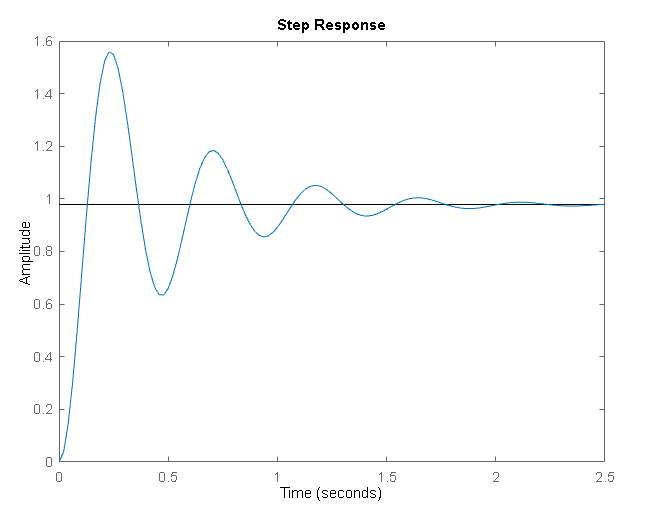
Ficando no Mathlab , conforme apresentado:
s=tf('s');
num6=[1];
den6=[1,2];
uGp6=tf(num6,den6);
num7=[1];
den7=[1,2];
mGp7=tf(num7,den7);
G8=series(uGp6,mGp7);
ft9=feedback(G8,1);
impulse(ft9);
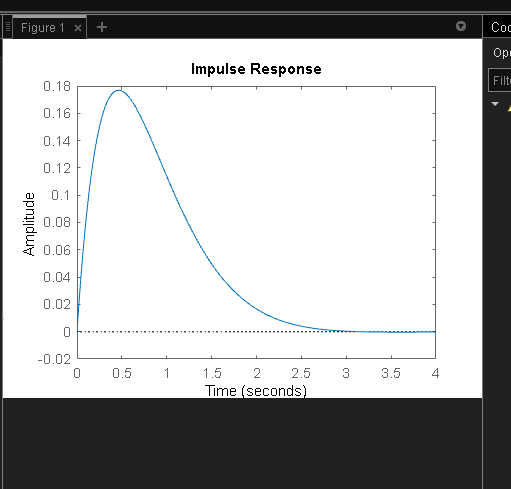
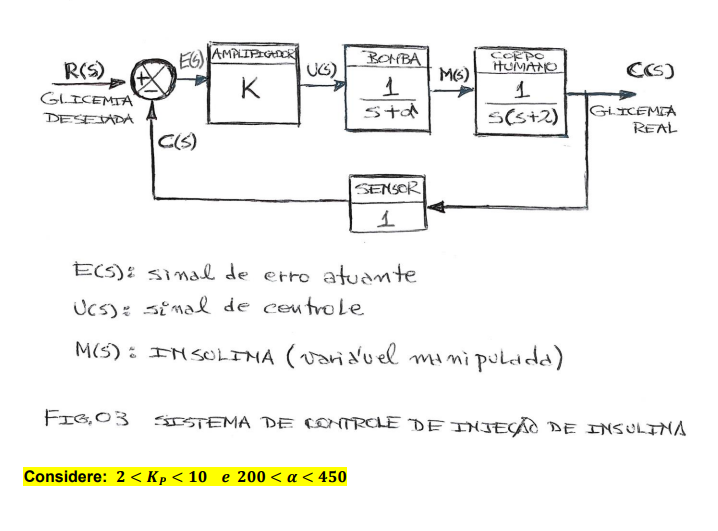
Considerando o Kp ; 2< Kp < 10
e 200 < a 450
Considerando kp=2, e a =200
s=tf('s');
num6=[1];
a=200;
den6=[1,a];
uGp6=tf(num6,den6);
num7=[1];
den7=[1,2];
mGp7=tf(num7,den7);
G8=series(uGp6,mGp7);
G9= Kp*G8;
ft9=feedback(G9,1);
impulse(ft9);
Uma das formas clássicas de se fazer o controle de potência de uma cavidade laser e mostrada na figura 47. O Diodo laser de bombeio, o cristal laser e o cristal SHG formam a cavidade laser. Através da injeção corrente no diodo de bombeio é possível obter um feixe de laser amarelo. O controle da cavidade é efetuado por dois controladores PI ( Proporcional integrative) (OGOTA,2003), PI 1 e P3, ligados numa configuração do tipo cascata ( SEDRA et a.,2007). A malha de controle formada pelo sensor HALL (sensor corrente), PI e 3 MOSFET ( field-effect transitor) (SEDRA.,2007) garante que o diodo bombeie o cristal com uma potência óptica proporcional ao sinal de referência aplicado na entrada da malha de controle. Para evitar flutuações de potência na saída da cavidade, existe uma malha de controle externa que capta uma percentagem da potência atraves do fotodiodo e realimenta o controlador PI 3.O resultado dessa topologia é a relação linearmente proporcional entre a referência de tensão gerada pelo microcontrolador e a potência óptica na saída da cavidade.
Essa arquitetura de controle possui algumas limitações quando se necessita geral pulso da ordem microssegundos. A primeira causa é o atraso gerado pelo PI 3 e PI 1, visto que a saída de um controlador é usada como entrada para outro. A segunda causa é a fonte de alimentação que possui um tempo de resposta a variação de uma carga muito lenta que pode chegar 1ms, quando utilizada a potência máxima da fonte. A terceira causa é a indutância dos cabos de alimentação do diodo laser que responde a variação da corrente com uma variação de tensão parasita. Cargas sensíveis tais como diodo laser são susceptíveis a essas variações e podem ter junção PN danificada. Essa topologia é adotada no controle do laser no modo normal de aplicação laser (regime continuo), no qual os pulso possuem duração longa, entre 50ms e 1000ms.
