O Efeito Elétrico no Organismo
Apresentação de Projeto de Leitor de ECG, da FATEC RP
Parte do material é fruto de pesquisa em IA e busca de artigos.
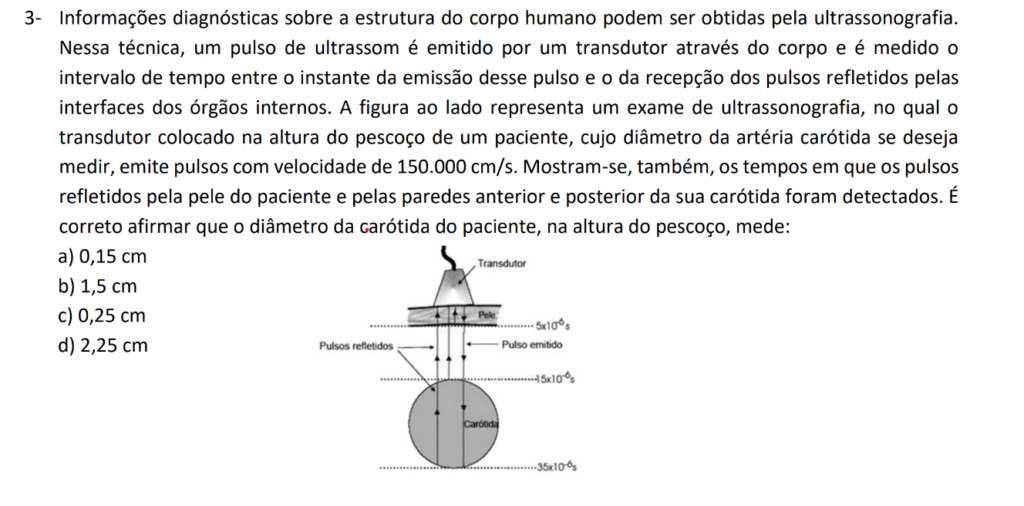
O corpo humano é uma intricada máquina que depende de fenômenos elétricos em diversas funções, desde os batimentos cardíacos até a atividade cerebral.
Instrumentos, como o Eletrocardiograma (ECG) e o Eletroencefalograma (EEG), são fundamentais para capturar e interpretar essa atividade elétrica.
Neste artigo, exploraremos a natureza da atividade bioelétrica e a eletrônica envolvida na sua detecção.
Neste artigo, discutiremos o efeito elétrico inerente ao organismo e a eletrônica envolvida na sua detecção através do ECG.
1. Geração de Sinais Elétricos no Organismo
A geração de sinais elétricos no corpo humano é um fenômeno biofísico que ocorre predominantemente devido ao movimento de íons através das membranas celulares.
Esta movimentação é governada por processos químicos e físicos que podem ser descritos matematicamente.
1.1. Efeito Elétrico no Organismo
O coração, sendo uma bomba muscular, não apenas realiza atividade mecânica, mas também gera atividade elétrica a cada batimento.
Esta atividade é o resultado do movimento coordenado de íons através das membranas celulares dos miócitos cardíacos.
1.2 Equilíbrio Químico e Potencial de Membrana
Cada célula, seja ela um neurônio, miócito cardíaco ou fibra muscular, mantém um potencial de membrana em repouso.

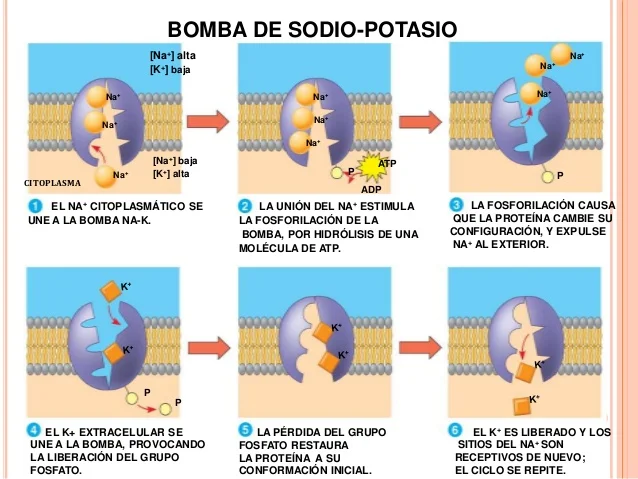
Este potencial de repouso é principalmente mantido pelas bombas de sódio-potássio (Na+/K+ ATPase) que transportam ativamente três íons de sódio para fora da célula e dois íons de potássio para dentro.
Equação de Nernst:
Onde:
- E é o potencial de equilíbrio do íon
- R é a constante dos gases
- T é a temperatura em Kelvin
- z é a valência do íon
- F é a constante de Faraday
1.3 Potenciais de Ação e a Propagação do Sinal Elétrico
Quando uma célula é excitada, os canais iônicos na membrana celular se abrem, permitindo que os íons entrem ou saiam da célula. Esta movimentação iônica gera o potencial de ação, que pode ser representado por uma série de fases na forma de um gráfico.
1.3 Potenciais de Ação no coração e sua aplicação
O estímulo elétrico começa nas células marcapasso do nó sinusal. Estas células geram um potencial de ação que se propaga pelas câmaras cardíacas.
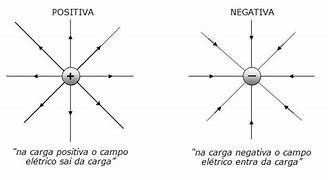
A despolarização é o fluxo de íons positivos para dentro da célula, gerando uma corrente elétrica que se propaga pelo coração.
A subsequente repolarização retorna as células ao seu estado polarizado original.

1.31 Geração do Sinal Elétrico
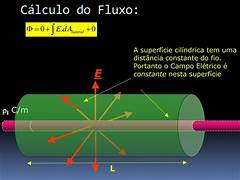
A atividade elétrica cardíaca é o resultado da soma vetorial das correntes elétricas geradas por inúmeras células cardíacas.

Esta corrente move-se de uma maneira que pode ser representada como um vetor, produzindo ondas de despolarização e repolarização que podem ser detectadas na superfície do corpo.

2. Eletrônica do ECG
O ECG utiliza eletrodos colocados na superfície da pele para medir a diferença de potencial elétrico entre diferentes pontos, que são sensíveis às correntes elétricas geradas pelo coração.
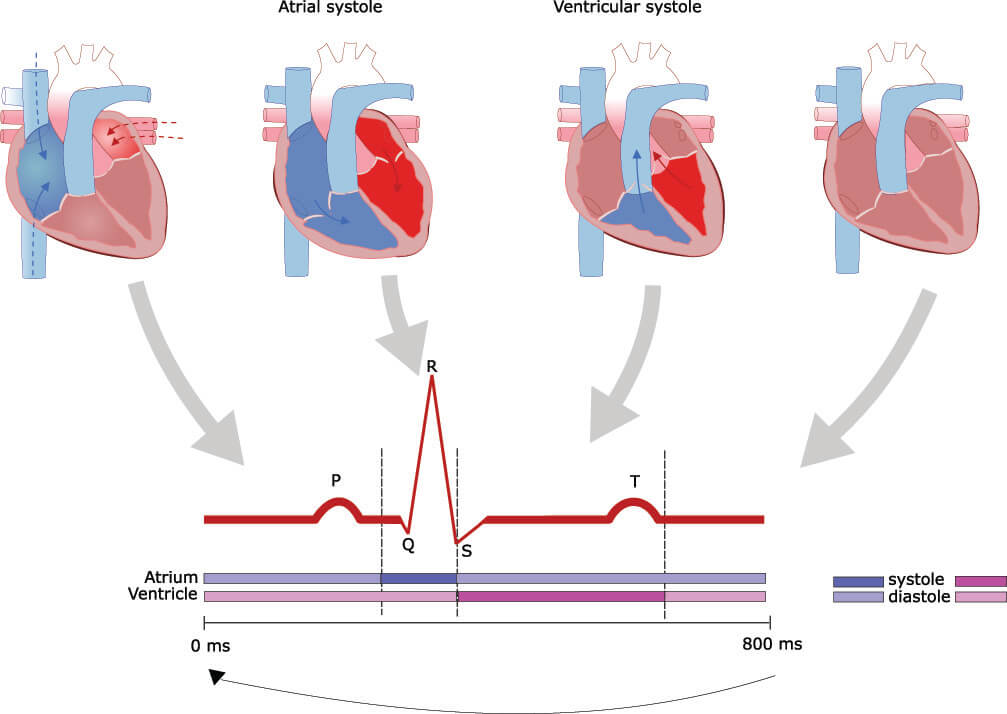
2.1 Captura de Sinais Elétricos
Os sinais elétricos gerados no corpo podem ser capturados utilizando eletrodos que detectam diferenças de potencial.

Os eletrodos medem a voltagem (V) gerada, que é a diferença de potencial entre dois pontos.
V=I*R
Onde:
- I é a corrente (medida em amperes)
- R é a resistência (medida em ohms)
O sinal elétrico capturado, por ser pequeno e suscetível a ruído, muitas vezes requer amplificação e filtragem para garantir uma análise precisa.
Estes ruídos podem ter origens diversas, como interferência de equipamentos elétricos próximos, atividade muscular ou movimentação do paciente.
Assim, a filtragem torna-se uma etapa crucial no processamento dos sinais capturados.
Filtros Passa-Baixa
Um filtro passa-baixa permite que sinais com uma frequência abaixo de um certo ponto de corte passem sem serem atenuados, enquanto sinais com frequência acima desse ponto são atenuados. No contexto da captura de sinais elétricos biológicos, este tipo de filtro pode ser utilizado para eliminar ruídos de alta frequência, como interferências de equipamentos elétricos ou atividade muscular de alta frequência.
Filtros Passa-Alta
Contrário ao filtro passa-baixa, o filtro passa-alta atenua sinais com frequência abaixo de um ponto de corte específico e permite que sinais de frequência mais alta passem.
Esse filtro é útil para eliminar ruídos de baixa frequência, como a deriva da linha de base no ECG devido ao movimento lento da pele e eletrodos ou a influência da respiração sobre a amplitude do sinal.
2.1 Eletrodos e Derivações
No ECG padrão, eletrodos são dispostos em combinações específicas chamadas de derivações. Estas derivações captam a atividade elétrica do coração de diferentes ângulos, fornecendo uma visão tridimensional da atividade elétrica cardíaca.
2.2 Interferências e Artefatos
A atividade muscular esquelética, equipamentos elétricos próximos e a própria condição da pele podem interferir na captação dos sinais pelo ECG. Por isso, o cuidado no posicionamento e fixação dos eletrodos é fundamental.
Técnicas de Filtragem de Ruídos
Existem diversas técnicas empregadas para filtrar ruídos em sinais elétricos biológicos:
- Filtragem Adaptativa: Esta técnica usa um algoritmo que se ajusta dinamicamente para filtrar o ruído de um sinal. Pode ser particularmente útil quando o ruído não é constante.
- Notch Filter: Específico para eliminar ruídos em uma frequência particular, como o ruído da rede elétrica de 50 ou 60 Hz, que é comum em gravações elétricas.
- Filtragem por Média Móvel: Uma média simples dos pontos de dados em uma janela contínua que se move ao longo do sinal. Isso suaviza o sinal e pode ajudar a reduzir picos de ruído de curta duração.
- Transformada de Fourier: Uma técnica que transforma o sinal do domínio do tempo para o domínio da frequência. Isso permite que as frequências específicas de ruído sejam identificadas e eliminadas antes de transformar o sinal de volta para o domínio do tempo.
3. Apresentação prática de captura
Base desta pesquisa:
Autor técnico do projeto arduino:
https://how2electronics.com/ecg-monitoring-with-ad8232-ecg-sensor-arduino/#comments
3.1 Apresentação do Equipamento
Usaremos para a apresentação o equipamento AD8232:

Neste vídeo apresento detalhes sobre o equipamento.
3.2 Conexão
A conexão com o equipamento utiliza as seguintes ligações.


3.3 Especificações técnicas
- Equipamento: AD8232 ecg measurement pulse heart ecg monitoring sensor
- Temperatura de Operação: -40-+85C
- Tensão de Alimentação: 3.3V ou 5V
- Nome da marca:Si Tai&SH
3.4 Modo de colocação
Utilizaremos o modo da direita, para apresentar as leituras.
Fonte do Projeto referencia na bibliografia how2eletronics
void setup() {
// initialize the serial communication:
Serial.begin(9600);
pinMode(10, INPUT); // Setup for leads off detection LO +
pinMode(11, INPUT); // Setup for leads off detection LO -
}
void loop() {
if((digitalRead(10) == 1)||(digitalRead(11) == 1)){
Serial.println('!');
}
else{
// send the value of analog input 0:
Serial.println(analogRead(A0));
}
//Wait for a bit to keep serial data from saturating
delay(1);
}Código do programa processing 4.3
import processing.serial.*;
Serial myPort; // The serial port
int xPos = 1; // horizontal position of the graph
float height_old = 0;
float height_new = 0;
float inByte = 0;
int BPM = 0;
int beat_old = 0;
float[] beats = new float[500]; // Used to calculate average BPM
int beatIndex;
float threshold = 620.0; //Threshold at which BPM calculation occurs
boolean belowThreshold = true;
PFont font;
void setup () {
// set the window size:
size(1000, 400);
// List all the available serial ports
println(Serial.list());
// Open whatever port is the one you're using.
myPort = new Serial(this, Serial.list()[0], 9600);
// don't generate a serialEvent() unless you get a newline character:
myPort.bufferUntil('\n');
// set inital background:
background(0xff);
font = createFont("Ariel", 12, true);
}
void draw () {
//Map and draw the line for new data point
inByte = map(inByte, 0, 1023, 0, height);
height_new = height - inByte;
line(xPos - 1, height_old, xPos, height_new);
height_old = height_new;
// at the edge of the screen, go back to the beginning:
if (xPos >= width) {
xPos = 0;
background(0xff);
}
else {
// increment the horizontal position:
xPos++;
}
// draw text for BPM periodically
if (millis() % 128 == 0){
fill(0xFF);
rect(0, 0, 200, 20);
fill(0x00);
text("BPM: " + inByte, 15, 10);
}
}
void serialEvent (Serial myPort)
{
// get the ASCII string:
String inString = myPort.readStringUntil('\n');
if (inString != null)
{
// trim off any whitespace:
inString = trim(inString);
// If leads off detection is true notify with blue line
if (inString.equals("!"))
{
stroke(0, 0, 0xff); //Set stroke to blue ( R, G, B)
inByte = 512; // middle of the ADC range (Flat Line)
}
// If the data is good let it through
else
{
stroke(0xff, 0, 0); //Set stroke to red ( R, G, B)
inByte = float(inString);
// BPM calculation check
if (inByte > threshold && belowThreshold == true)
{
calculateBPM();
belowThreshold = false;
}
else if(inByte < threshold)
{
belowThreshold = true;
}
}
}
}
void calculateBPM ()
{
int beat_new = millis(); // get the current millisecond
int diff = beat_new - beat_old; // find the time between the last two beats
float currentBPM = 60000 / diff; // convert to beats per minute
beats[beatIndex] = currentBPM; // store to array to convert the average
float total = 0.0;
for (int i = 0; i < 500; i++){
total += beats[i];
}
BPM = int(total / 500);
beat_old = beat_new;
beatIndex = (beatIndex + 1) % 500; // cycle through the array instead of using FIFO queue
}3.5 Apresentação do autor do software:
3.6 Visão Geral de um projeto de ECG
Apesar de apresentarmos uma visão geral, um ECG não é somente seu sensor, de fato ele é formado por uma série de equipamentos que compoem dos demais membros do ECG.
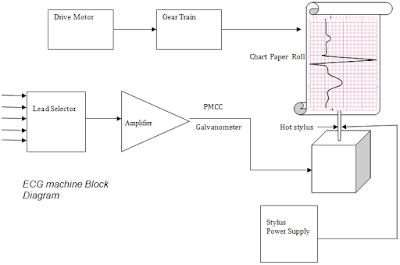
1. Eletrodos: Sabemos que os eletrodos de ECG usados principalmente para a captação de ECG são em número de cinco. Colocando esses eletrodos em partes apropriadas do corpo.
2. Seletor de leads: conforme dito anteriormente, cada par de leads transmite certas informações. Portanto, para a forma de onda ou visualização apropriada, temos que selecionar um par de derivações apropriado. O par de derivações pode ser selecionado por uma chave seletora de derivações que pode ser alternada para diferentes pares de derivações de acordo com o tipo de forma de onda necessária.
3. Pré-amplificador: O sinal de ECG apresenta níveis de amplitude muito fracos. Portanto, é necessário que, para fins adequados de análise e plotagem, a forma de onda seja amplificada. O pré-amplificador aqui utilizado será um amplificador operacional ou amplificador de instrumentação de alto ganho. Eles têm alto CMRR e impedância de entrada extremamente alta.
4. Driver: Usamos um motor driver de especificação adequada para acionar o rolo de papel. Normalmente, a forma de onda do ECG deve ser plotada em um papel gráfico móvel para descobrir as irregularidades (se houver) nas regiões P, Q, R, S, T e U da forma de onda do ECG. pode ser controlado pelo motor do acionador, que alimenta o gatilho do rolo.
5. Galvanômetro PMMC: O galvanômetro PMMC (Permanent Magnet Moving Coil) é um tipo especial de dispositivo, onde a deflexão da bobina depende da amplitude e da polaridade do sinal aplicado à sua entrada. A ponta de escrita da caneta hot tip está conectada ao papel quadriculado. Portanto, a caneta estará em repouso no centro de seu percurso quando nenhuma corrente fluir na bobina. Portanto, a direção da deflexão na bobina e a quantidade de deflexões são determinadas pela amplitude e polaridade da forma de onda do ECG.
6. Caneta de ponta quente e aquecedor de ponta: Nas técnicas de gravação de ECG mais comuns, usamos caneta de ponta quente para escrita térmica. Isso ocorre porque normalmente usamos gravadores térmicos para traçar formas de onda. A caneta é mantida sempre quente pela fonte de alimentação do aquecedor da caneta. A ponta de escrita é uma caneta aquecida por um fio de resistência.
7. Registradores: Conforme discutido agora, geralmente usamos gravadores térmicos para a representação da forma de onda do ECG. O papel utilizado nos registradores térmicos é de um material especial que fica preto quando aquecido. A ponta quente da caneta deixará o papel branco preto sempre que tocar. A ponta da caneta se move de acordo com o movimento da bobina que, por sua vez, é proporcional à amplitude e polaridade da forma de onda do ECG. Como a ponta da caneta está em contato com o registrador gráfico térmico, é obtida uma representação clara da forma de onda do ECG.
3.7 Tipos de Leituras

4. Conclusão
O coração gera atividade elétrica através da movimentação de íons durante seus ciclos de despolarização e repolarização. Esta atividade pode ser detectada e interpretada através do ECG, uma ferramenta valiosa para a avaliação não invasiva da função cardíaca.
Compreender o efeito elétrico intrínseco ao nosso organismo e a tecnologia por trás da sua captura é crucial para a correta avaliação clínica dos pacientes.