Trabalho de Óptica – Equipamentos Oftalmológicos
Equipe 2
- Luis Felipe Fadel
- Luiz Cezar da Silva
- Achilles Marcelo Bermudes
- Marcelo Maurin Martins
- Jose Servulo
Visão Geral
Introdução à Óptica Oftalmológica:
O que é Óptica Oftalmológica?
A óptica oftalmológica é um ramo da medicina e da física que se concentra no estudo e manejo da luz em relação ao olho humano. Ela abrange o entendimento de como a luz é refratada, absorvida e refletida pelo olho, além de como estas interações afetam a visão. A óptica oftalmológica é fundamental para o desenvolvimento de lentes corretivas, óculos, lentes de contato e para a realização de cirurgias refrativas.
Evolução Histórica dos Equipamentos Ópticos em Oftalmologia
Inícios Antigos
Primeiros Óculos (Século 13):
A história dos equipamentos ópticos oftalmológicos começa com a invenção dos primeiros óculos na Itália no século 13. Estes eram basicamente lentes simples montadas em armações que ajudavam na correção de problemas de visão relacionados à idade, como a presbiopia.
Avanços no Renascimento
Desenvolvimento das Lentes Convexas e Côncavas (Século 15 e 16):
Durante o Renascimento, houve avanços significativos no design e na fabricação de lentes. Cientistas como Leonardo da Vinci e Johannes Kepler contribuíram para a compreensão de como as lentes podiam corrigir a visão e começaram a explorar o uso de lentes convexas e côncavas para tratar miopia e hipermetropia.
Revolução Científica
Invenção do Oftalmoscópio (1851):
Um marco importante foi a invenção do oftalmoscópio por Hermann von Helmholtz em 1851. Este dispositivo permitiu, pela primeira vez, a visualização direta do interior do olho, revolucionando o diagnóstico de doenças oculares.
Era Moderna
Inovações do Século 20:
No século 20, a tecnologia oftalmológica avançou rapidamente. Foram introduzidos equipamentos como a lâmpada de fenda, permitindo exames detalhados da frente do olho, e a tomografia de coerência óptica (OCT), uma inovação do final do século 20, que fornece imagens detalhadas das camadas da retina.
Tecnologia Laser e Além
Avanços em Cirurgia Refrativa (Final do Século 20 e 21):
A introdução do laser em oftalmologia transformou os procedimentos cirúrgicos, com técnicas como LASIK e fotocoagulação a laser tornando-se comuns para o tratamento de erros refrativos e doenças como a retinopatia diabética.
Destaque a evolução histórica dos equipamentos ópticos usados em oftalmologia.
Tipos de Equipamentos Oftalmológicos:
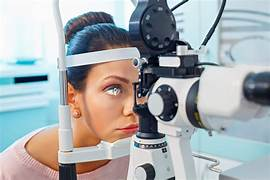
Lâmpada de Fenda (Biomicroscópio):
O que é a Lâmpada de Fenda?
A lâmpada de fenda, também conhecida como biomicroscópio, é um instrumento fundamental na oftalmologia. Ela consiste em uma fonte de luz intensa que pode ser focalizada para formar uma “fenda” estreita e uma série de lentes microscópicas. Este equipamento é usado para observar o olho humano em detalhes significativos, permitindo a visualização de estruturas desde a córnea até a retina.
Funcionamento da Lâmpada de Fenda
Iluminação Focalizada:
A luz da lâmpada de fenda é direcionada para o olho em um feixe estreito, o que permite examinar diferentes partes do olho em detalhes.
Ampliação: As lentes microscópicas aumentam as estruturas oculares, tornando mais fácil para o oftalmologista detectar anormalidades.
Diagnóstico de Condições Oculares
Exame da Superfície Ocular:
A lâmpada de fenda é usada para examinar a córnea, a conjuntiva e a íris, ajudando a diagnosticar condições como úlceras corneanas, conjuntivite e iridociclite.
Avaliação do Segmento Anterior:
É possível avaliar o cristalino e o humor aquoso, detectando cataratas e sinais de glaucoma.
Inspeção do Segmento Posterior:
Embora menos comum, a lâmpada de fenda também pode ser usada para examinar o segmento posterior do olho, especialmente quando combinada com lentes especiais, para avaliar a retina e o nervo óptico.
Importância Clínica
Detecção Precoce:
O uso da lâmpada de fenda permite a detecção precoce de muitas doenças oculares, essencial para tratamentos bem-sucedidos.
Monitoramento de Tratamentos:
Também é útil no monitoramento de respostas a tratamentos, como a evolução de uma úlcera corneana ou a eficácia de um tratamento para glaucoma.
Retinoscópio
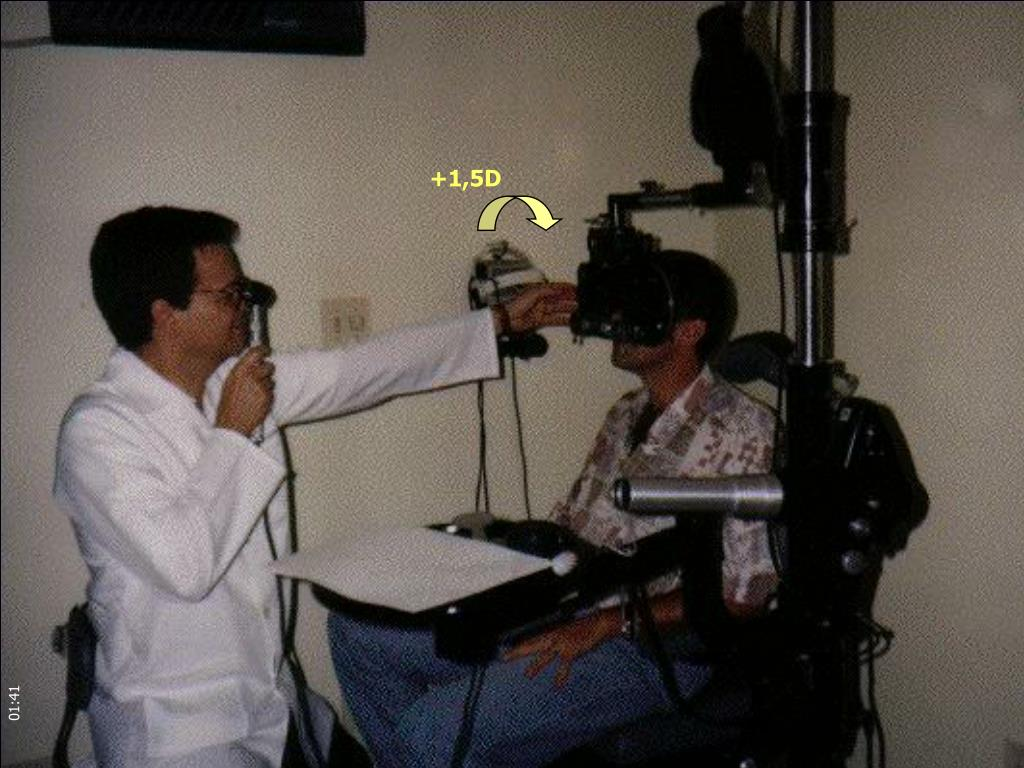
O que é um Retinoscópio?
O retinoscópio é um instrumento oftalmológico usado para medir o erro refrativo do olho, como miopia, hipermetropia e astigmatismo. Ele projeta um feixe de luz no olho e observa a reflexão (reflexo) da luz da retina.
Princípios de Funcionamento
Reflexo Retiniano:
O retinoscópio avalia como o reflexo da luz se move na retina do paciente. Este movimento é analisado para determinar se o olho é emétrope (sem erro refrativo), míope (curto), hipermetrope (longo) ou astigmático.
Neutralização do Reflexo:
O objetivo do exame é “neutralizar” o reflexo retiniano com o uso de lentes de teste, determinando assim o erro refrativo.
Características do Retinoscópio
- Fonte de Luz e Espelho: Equipado com uma fonte de luz e um espelho que pode ser ajustado, permitindo que o médico direcione a luz para o olho do paciente.
- Tipos: Existem dois tipos principais de retinoscópios: de faixa e de ponto, diferenciando-se pelo tipo de feixe de luz que projetam.
Uso do Retinoscópio
- Exame Inicial: Geralmente é usado como um exame inicial para estimar o erro refrativo antes de realizar testes mais detalhados.
- Pacientes de Todas as Idades: É especialmente útil para examinar crianças pequenas ou pacientes que não conseguem responder a um exame de refração padrão.
Aplicações Clínicas
Determinação de Prescrições de Óculos: Essencial para formular prescrições de óculos ou lentes de contato.
Detecção de Astigmatismo:
Permite a detecção precisa de astigmatismo e sua orientação.
Avaliação em Casos Especiais:
Útil em casos onde a refração automatizada não é aplicável ou eficaz.
Vantagens do Retinoscópio
Independente de Resposta Subjetiva:
Como o instrumento não depende das respostas do paciente, é ideal para uso em pacientes não verbais ou com dificuldade de comunicação.
Flexibilidade e Precisão:
Oferece uma forma flexível e precisa de medir o erro refrativo, especialmente em situações pré-clínicas ou em comunidades com acesso limitado a equipamentos mais sofisticados.
Desafios e Limitações
Habilidade do Examinador:
Requer prática e habilidade para interpretar corretamente o reflexo retiniano.
Influência de Condições Oculares:
Condições como opacidades da córnea ou cataratas podem afetar a precisão do exame.
Oftalmoscópio:
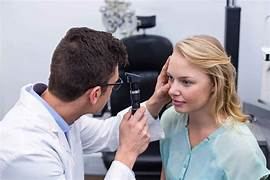
Introdução ao Oftalmoscópio
O oftalmoscópio é um instrumento fundamental em oftalmologia, desenhado para examinar o fundo do olho. Ele permite aos médicos visualizar estruturas internas como a retina, o disco óptico e os vasos sanguíneos, essencial para diagnosticar e monitorar uma variedade de condições oculares.
Princípios de Funcionamento
Iluminação e Lentes:
O oftalmoscópio possui uma fonte de luz e um sistema de lentes que ajudam a iluminar e visualizar o interior do olho.
Ajuste de Foco:
As lentes podem ser ajustadas para compensar a refração do olho do paciente, permitindo uma visão clara das estruturas retinianas.
Visualização do Fundo do Olho
Retina:
Através do oftalmoscópio, a retina pode ser examinada detalhadamente, permitindo a identificação de anormalidades como degeneração macular, descolamento de retina e danos causados pela retinopatia diabética.
Disco Óptico:
Este é o ponto onde o nervo óptico entra no olho, sendo crucial na avaliação de condições como glaucoma e neuropatias ópticas.
Vasos Sanguíneos:
A avaliação dos vasos sanguíneos retinianos é vital para detectar problemas vasculares, como oclusões vasculares e hipertensão ocular.
Tipos de Oftalmoscópios
Oftalmoscópios Diretos:
Mais comumente usados, proporcionam uma imagem detalhada e aumentada do fundo do olho.
Oftalmoscópios Indiretos:
Usados para obter uma visão mais ampla do fundo do olho, são essenciais para examinar a periferia retiniana.
Usos Clínicos do Oftalmoscópio
Diagnóstico de Doenças Oculares:
Instrumental no diagnóstico de doenças como glaucoma, retinopatia diabética e degeneração macular.
Monitoramento de Doenças Sistêmicas:
Condições como diabetes e hipertensão podem afetar os vasos sanguíneos retinianos, tornando o oftalmoscópio útil no monitoramento dessas doenças.
Importância na Oftalmologia
Detecção Precoce de Condições Oculares:
Permite a identificação precoce de anormalidades oculares, o que é crucial para tratamentos eficazes.
Ferramenta de Ensino:
Também é uma ferramenta valiosa para o ensino e a formação de estudantes de medicina e oftalmologistas em treinamento.
Tecnologias Avançadas em Óptica Oftalmológica:
Tomografia de Coerência Óptica (OCT)
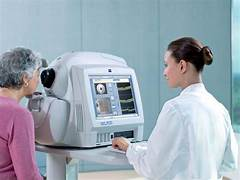
O que é OCT?:
A tomografia de coerência óptica (OCT) é uma tecnologia de imagem não invasiva que usa ondas de luz para capturar imagens bidimensionais de alta resolução das camadas da retina. Ela fornece uma visão em camadas, quase histológica, do tecido retiniano.
Funcionamento:
Utiliza a interferometria de luz para obter imagens detalhadas. A luz é projetada no olho e as reflexões são medidos, criando uma imagem detalhada da estrutura retiniana.
Aplicações Clínicas:
Essencial no diagnóstico e monitoramento de doenças como degeneração macular, edema macular, buraco macular, e descolamento de retina. Também é usada para avaliar a eficácia de tratamentos e acompanhar a progressão de doenças oculares.
Fotocoagulação a Laser

Definição:
A fotocoagulação a laser é um procedimento que usa a energia do laser para tratar anormalidades específicas no olho. É um tratamento focado que visa a reparação e prevenção de danos a áreas-chave do olho.
Mecanismo de Ação: O laser é aplicado diretamente sobre as áreas afetadas da retina, causando uma queimadura controlada que sela vasos sanguíneos anormais ou repara tecidos danificados.
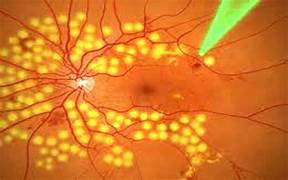
Uso em Retinopatia Diabética: Especialmente importante no tratamento da retinopatia diabética, onde ajuda a prevenir a perda de visão, selando vasos sanguíneos que podem vazar e causar danos à retina. Também é usada em outras condições, como rupturas ou descolamentos de retina.
Crucialidade da Precisão em Diagnósticos e Tratamentos

Precisão para Diagnósticos Corretos:
A precisão dos equipamentos ópticos oftalmológicos é essencial para garantir diagnósticos corretos. Erros mínimos podem levar a diagnósticos incorretos, resultando em tratamentos inadequados ou desnecessários.
Impacto nos Tratamentos:
Tratamentos eficazes dependem fortemente da precisão dos equipamentos utilizados. Na cirurgia refrativa, por exemplo, a precisão na medição do erro refrativo é vital para garantir resultados satisfatórios.
Desafios na Calibração e Manutenção de Equipamentos Ópticos
Complexidade dos Equipamentos:
Equipamentos oftalmológicos são intrincados e requerem calibrações precisas para funcionar corretamente.
Necessidade de Calibração Regular:
A calibração regular é crucial para manter a precisão. Isso inclui ajustes finos para garantir que as medições sejam consistentes e confiáveis.
Manutenção Preventiva:
A manutenção preventiva é necessária para identificar e corrigir problemas antes que eles afetem a precisão do equipamento.
Considerações na Calibração e Manutenção
Padrões e Protocolos:
É importante seguir padrões e protocolos estabelecidos para calibração e manutenção, garantindo que os equipamentos estejam sempre em conformidade com as especificações do fabricante.
Treinamento Especializado:
Operadores e técnicos precisam de treinamento especializado para realizar calibrações e manutenções corretamente.
Registros e Documentação:
Manter registros detalhados de calibrações e manutenções ajuda a monitorar a saúde dos equipamentos e identificar padrões ou problemas recorrentes.
Impacto da Tecnologia Avançada
Softwares de Calibração:
O uso de softwares avançados para calibração ajuda a aumentar a precisão e a eficiência.
Atualizações e Upgrades:
Manter os equipamentos atualizados com as últimas tecnologias e upgrades é importante para manter a precisão.
Estudos de Casos
Caso 1: Detecção Precoce de Glaucoma com Tomografia de Coerência Óptica (OCT)
- Situação: Uma paciente, com histórico familiar de glaucoma, realizou um exame de rotina onde a OCT foi utilizada.
- Diagnóstico: A OCT revelou uma diminuição sutil na espessura da camada de fibras nervosas da retina, um indicador precoce de glaucoma.
- Resultado: O diagnóstico precoce permitiu o início imediato do tratamento com colírios para reduzir a pressão intraocular, prevenindo danos significativos ao nervo óptico.
Caso 2: Tratamento de Retinopatia Diabética com Fotocoagulação a Laser
- Situação: Um paciente diabético apresentou sinais de retinopatia diabética em estágio inicial durante um exame de fundo de olho.
- Intervenção: Foi realizada a fotocoagulação a laser para selar os vasos sanguíneos anormais e prevenir o vazamento.
- Resultado: O tratamento estabilizou a condição do paciente, prevenindo a progressão para estágios mais graves da doença e a perda de visão.
Caso 3: Uso do Oftalmoscópio na Identificação de Descolamento de Retina
- Contexto: Um paciente chegou à clínica com queixas de “moscas volantes” e uma sombra em seu campo de visão.
- Diagnóstico: Utilizando o oftalmoscópio, o médico identificou um descolamento de retina.
- Tratamento: O paciente foi encaminhado imediatamente para cirurgia de retina, salvando sua visão.
Caso 4: Correção de Miopia Severa com Lâmpada de Fenda e Retinoscópio
- Situação: Um adolescente apresentava dificuldade de visão a distância, afetando sua performance acadêmica.
- Exame: Através do uso combinado da lâmpada de fenda e do retinoscópio, foi diagnosticada uma miopia severa.
- Solução: Óculos com lentes corretivas foram prescritos, resultando em uma melhora imediata da visão e qualidade de vida do paciente.
Caso 5: Diagnóstico de Catarata Usando Biomicroscopia com Lâmpada de Fenda
- Contexto: Uma idosa relatou diminuição da visão durante um exame de rotina.
- Diagnóstico: Com a ajuda da biomicroscopia com lâmpada de fenda, foi detectada uma catarata significativa.
- Intervenção: A paciente foi submetida a uma cirurgia de catarata bem-sucedida, restaurando sua visão.
Conclusão
- Ao examinar a evolução e a aplicação da óptica oftalmológica, fica evidente o impacto significativo que esta área tem no campo da saúde ocular. Desde as primeiras invenções de óculos no século 13 até as tecnologias avançadas de hoje, como a tomografia de coerência óptica (OCT) e a fotocoagulação a laser, a óptica oftalmológica tem sido um pilar fundamental na melhoria do diagnóstico e tratamento de condições oculares.
- A precisão dos equipamentos ópticos oftalmológicos, como o retinoscópio, o oftalmoscópio e a lâmpada de fenda, é crucial para diagnósticos precisos e tratamentos eficazes. Estes instrumentos permitem uma visualização detalhada e profunda do olho, revelando desde problemas de refração até condições mais sérias, como glaucoma e retinopatia diabética.
- Os avanços tecnológicos, especialmente a OCT e a fotocoagulação a laser, têm proporcionado novas possibilidades no tratamento de doenças oculares, permitindo intervenções mais precisas e menos invasivas. Estes avanços não apenas melhoraram a qualidade do cuidado ao paciente, mas também abriram novos caminhos para pesquisas futuras.
- Os estudos de caso demonstram a aplicabilidade prática e o impacto real destas tecnologias na vida dos pacientes. Eles ilustram como o uso adequado e preciso dos equipamentos ópticos pode levar a diagnósticos mais rápidos e tratamentos mais efetivos, muitas vezes salvando ou significativamente melhorando a visão dos pacientes.
- Em conclusão, a óptica oftalmológica é uma área dinâmica e em constante evolução, essencial para o avanço da medicina ocular. O contínuo desenvolvimento de novas tecnologias e técnicas representa uma esperança contínua para melhor diagnóstico, tratamento e prevenção de doenças oculares, impactando positivamente a saúde ocular global.
Referências
- Livros de Referência em Oftalmologia:
- Títulos como “Princípios e Prática de Oftalmologia”, “Atlas de Oftalmologia Clínica” e “Fundamentos de Oftalmologia” são excelentes fontes de informação abrangente sobre óptica oftalmológica e equipamentos.
- Artigos Científicos e Jornais de Oftalmologia:
- Artigos de periódicos como “American Journal of Ophthalmology”, “Journal of Refractive Surgery”, e “Ophthalmology”, que frequentemente publicam pesquisas sobre as últimas tecnologias e práticas em oftalmologia.
- Manuais e Guias Técnicos de Equipamentos:
- Guias de fabricantes de equipamentos oftalmológicos, como lâmpadas de fenda, retinoscópios e oftalmoscópios, fornecem informações detalhadas sobre a operação e a manutenção desses dispositivos.
- Publicações sobre História da Medicina e Oftalmologia:
- Livros e artigos que abordam a história da medicina e da oftalmologia, como “A History of Ophthalmology” por Julius Hirschberg, podem ser úteis para compreender a evolução histórica dos equipamentos ópticos.
- Recursos Online Educativos e Profissionais:
- Websites de organizações oftalmológicas respeitadas, como a Academia Americana de Oftalmologia (AAO) e a Sociedade Europeia de Catarata e Cirurgia Refrativa (ESCRS), que fornecem materiais educativos e atualizações sobre equipamentos e técnicas oftalmológicas.
- Publicações Sobre Avanços Tecnológicos em Oftalmologia:
- Artigos sobre inovações recentes como OCT e fotocoagulação a laser, disponíveis em jornais científicos especializados e conferências de oftalmologia.